Backtracking - Subsets II

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Medium

DFS, Pruning

Problem

Given an integer array nums that may contain duplicates, return all possible subsets (the power set).

The solution set must not contain duplicate subsets. Return the solution in any order.

Example 1:

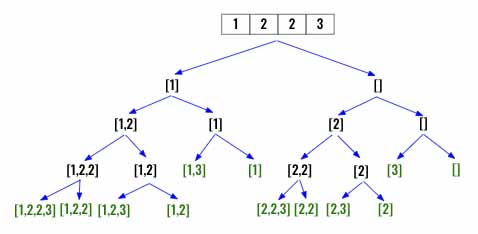
Input: nums = [1,2,2]
Output: [[],[1],[1,2],[1,2,2],[2],[2,2]]

Example 2:

Input: nums = [0]
Output: [[],[0]]

Solution

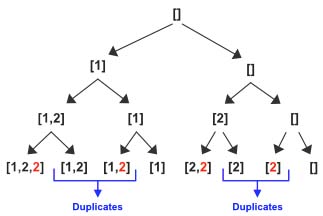
If we follow the exact same solution as Subsets, you will find two duplicates for the input array [1,2,2]. I have highlighted all the 2’s which were 3 in the Subsets problem as the input array changed from [1,2,3] to [1,2,2]

The solution we want is the following. The issue is after popping the value 2 from the subset we are incrementing the index again however since there is another 2 in the new index our results now has duplicates. We still want the previous results if the input is [1,2,3] instead of [1,2,2].

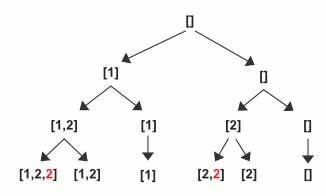
The way to resolve this is to increment index such a way it does not land in another 2 after popping 2 from the subset. The first step is to make sure the input array is sorted. This way all duplicates will be continuously repeated.

nums.sort()

Now, we can keep incrementing index until it finds a new value other than current nums[index] or reaches len(nums)-1. So in case of [1,2,2], after we pop 2 from subset and instead of calling dfs(index+1)= dfs(1+1) we keep incrementing index until it reaches len(nums)-1 and then we call dfs(index+1)= dfs(2+1). This way the terminating condition is triggered and [1] will be added to the output.

This way the highlighted traversal does not execute and the duplicate entry does not get added to the subset array.

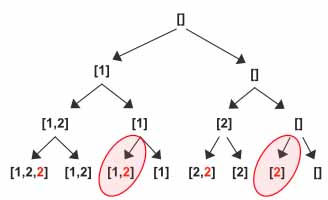
Here is another example of input array [1,2,2,3], when we come back to index=0, instead of incrementing it by +1 we shift it to 2+1.

Here is just 2 additional lines of code to add to the existing Subsets solution. The reason we are using ` < len(nums)-1 is, we have to compare with the next value so setting < len(nums) will cause out of bound exception and we are going to increment index when calling dfs()` anyway.

while index < len(nums)-1 and nums[index]==nums[index+1]:
  index+=1

And thats all the changes needed for this to work. If it’s not yet clear, my suggestion is to work out an example using on paper.

Final Code

Here is the full code.

def subsets(nums):
    output = []
    subset = []
    
    # Sort the values
    nums.sort()

    def dfs(index):
        if index >= len(nums):
            output.append(subset.copy())
            return

        subset.append(nums[index])
        dfs(index + 1)

        subset.pop()
        
        # Skip all the duplicates
        while index < len(nums)-1 and nums[index] == nums[index+1]:
            index+=1
            
        dfs(index + 1)

    dfs(0)
    return output