Dynamic Programming - Longest Increasing Subsequence

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

DP

Problem

Given an integer array nums, return the length of the longest strictly increasing subsequence.

Example 1:

Input: nums = [10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.

Example 2:

Input: nums = [0,1,0,3,2,3]
Output: 4

Example 3:

Input: nums = [7,7,7,7,7,7,7]
Output: 1

Solution

The requirement to move from left to right itself gives away the clue that this problem can be solved by moving in the opposite direction. We can use dfs() to solve this by constructing a tree and traversing to find out which path leads to the solution, however the thought process of solving using Dynamic Programming in this case is very intuitive.

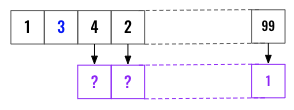
We are going to again try to find whats needed for an element at index i to be part of the largest increasing sub-sequence ? Below is an example where we are trying find out whats the longest strictly increasing subsequence from index 1, that is number 3.

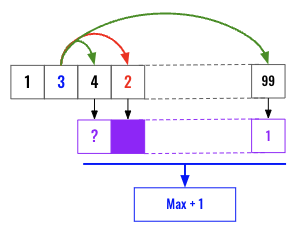
Now if we already know the longest strictly increasing subsequence from each of the elements of the right of 3, then we can just loop through that (shown in purple color) array or map object and find the max value of those where the current number 3 is smaller than the respective element .

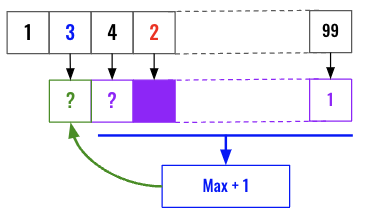
Let’s see that visually, we have a second loop to iterate all the elements at the right of 3. We are going to discard if any element that is smaller than 3. In this case, 2 is smaller, so we do not need its longest strictly increasing subsequence so we masked that out in the purple array. (Cache). At the end we find the max and increment it by 1 for finding out the longest strictly increasing subsequence including 3.

Finally we set the longest strictly increasing subsequence value for 3 in our cache (purple array) and process the previous number 1.

Start with defining the purple array as our cache for the dynamic programming. Now each value by them self is automatically part of a subsequence of length 1 so lets initialize the array with all 1s.

cache = [1] * len(nums)

Now start the outer loop to traverse our nums array from back. The last element will always have associated longest strictly increasing subsequence value as 1 so we can skip that and start from the element prior to that. (Hence -2 below)

for i in range(len(nums)-2,-1,-1)

For each of the element at index i we need to traverse till end of the array and collect the longest strictly increasing subsequence number for any element larger than the current index value.

for i in range(len(nums)-2,-1,-1):
  lsis_so_far =[1]
  for j in range(i+1, len(nums)):
    if nums[i] < nums [j]:
      lsis_so_far.append(cache[j])
  cache[i]=1+max(lsis_so_far)
  

Now, we will not write like this way as we can always have a rolling max than need to store all of the values to a temporary lsis_so_far array.

for i in range(len(nums)-2,-1,-1):
  for j in range(i+1, len(nums)):
    if nums[i] < nums[j]:
      cache[i]= max(cache[i],cache[j]+1)            

Finally return the max from the cache. We can also use a rolling max here, however does not really change the outcome in LeetCode.

return max(cache)

Final Code

Here is the full code.

def longest_strictly_increasing_subsequence(nums):
    cache = [1] * len(nums)
    for i in range(len(nums)-2, -1, -1):
        for j in range(i+1, len(nums)):
            if nums[i] < nums[j]:
                cache[i] = max(cache[i], cache[j]+1)
    return max(cache)