Backtracking - Subsets

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

DFS

Problem

Given an integer array nums of unique elements, return all possible subsets (the power set).

The solution set must not contain duplicate subsets. Return the solution in any order.

Example 1:

Input: nums = [1,2,3]
Output: [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

Example 2:

Input: nums = [0]
Output: [[],[0]]

Solution

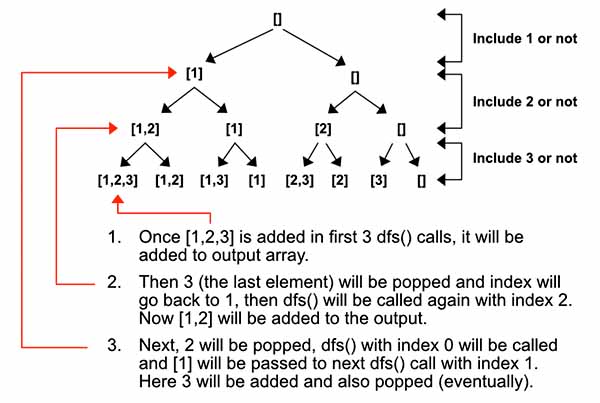
This is one of the classic backtracking algorithm. For every index location, we need to run dfs() twice. One using the element and another time is not using the element. Let’s look at the graph below.

Start by defining the variables. We need two of them, one for returning the final output and another one for saving the subset.

output = []
subset = []

Next the most important part is to identify the terminating condition, that is when to add the current subset to the output array. Whenever we reach the end of the tree, that is the index is equal to the len(nums) we know that we have reached a leaf and now need to add the subset to the output.

def dfs(index):
  if index >= len(nums):
    output.append(subset.copy())
    return

Now the recursive calls.

  subset.append(nums[index])
  dfs(index + 1)

  subset.pop()
  dfs(index + 1)

Now call the dfs() by passing index as 0 and return the output.

dfs(0)
return output

Reverse Way!

Can you now implement the reverser way? So instead of adding the nums[index] value to the subset and popping it later. Start without the subset.append(nums[index]) and add it in the second choice. Below is the code:

	...
	
  # Call dfs() without appending the nums[i]
	dfs(index + 1)
  	
  # now add it and call dfs()
  subset.append(nums[index])
  dfs(index + 1)
	
  # before returning still need to pop it.
  subset.pop()

Final Code

Here is the full code.

def subsets(nums):
    output = []
    subset = []

    def dfs(index):
        if index >= len(nums):
            output.append(subset.copy())
            return

        subset.append(nums[index])
        dfs(index + 1)

        subset.pop()
        dfs(index + 1)

    dfs(0)
    return output