Backtracking - Permutations

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Medium

Recursive

Problem

Given an array nums of distinct integers, return all the possible permutations. You can return the answer in any order.

Example 1:

Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

Example 2:

Input: nums = [0,1]
Output: [[0,1],[1,0]]

Example 3:

Input: nums = [1]
Output: [[1]]

Solution

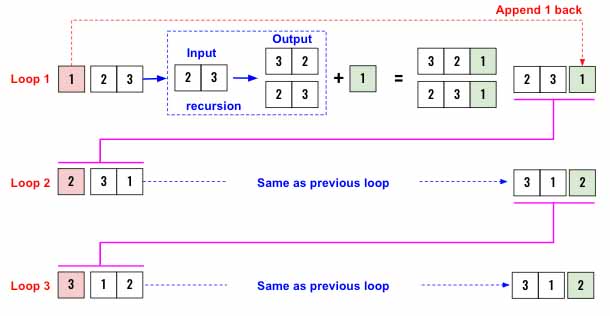
Let’s look at solving the problem visually first. We will use Example 1 and will be running a recursive algorithm to solve this. Below diagram explains the high level design of it. We are going to have an output list which we will populate all the combinations.

• We will have a for loop to run len(nums) times to generate all the combinations.

for index in range(len(nums)):

• In the diagram below in the left all 3 Loops are depicted. In start of loop 1, we will remove the element 1 at index 0 from the list.

  first = nums.pop(0)

• Then take the remaining two elements ([2,3]) and invoke a recursive algorithm.

  permutation_arr = recursive_function(nums)

• We should design the recursive algorithm so that it returns an array with two combinations [[3,2],[2,3]].

• Now we append the removed element 1 at the end of the returned list. So the output becomes [[3,2,1],[2,3,1]]. Add these to the output array.

  for perm in permutation_arr:
    perm.append(first)

• Add the updated permutation_arr into the output.

  output.extend(permutation_arr)

• Then add 1 back to the original input list. This is the trick to understand. Now the array has been shifted by 1 and in loop 2, 2 will be picked as the first element to be removed.

  nums.append(first)

Here is the python code for the same.

for index in range(len(nums)):
  first = nums.pop(0)
  
  permutation_arr = recursive_function(nums)
  for perm in permutation_arr:
    perm.append(first)
  
  output.extend(permutation_arr)
  nums.append(first)

If we pass just one element to the recursion program, we can just return that. This will be the base case.

if len(nums) == 1:
  return [nums.copy()]

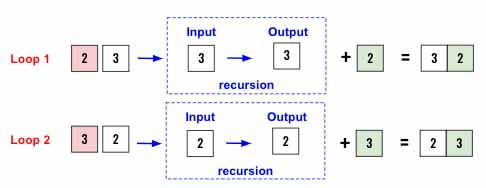
So let’s see how the base case going to work. From the Loop 1, of the previous diagram we are invoking the recursive_function by passing [2,3]. Below is the same diagram using [2,3] as an input and generating the [[3,2],[2,3]] as output. As we see, in the base case the same element is getting returned.

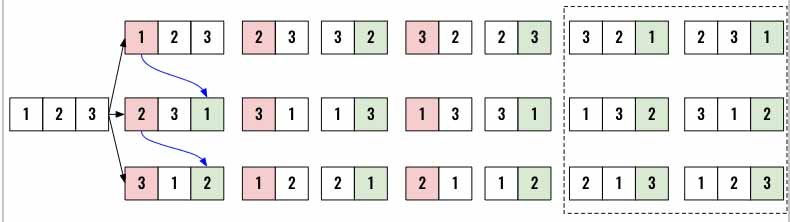
We will keep continuing this way until the loop ends (Referring back the first diagram). This should generate all 6 combinations needed.

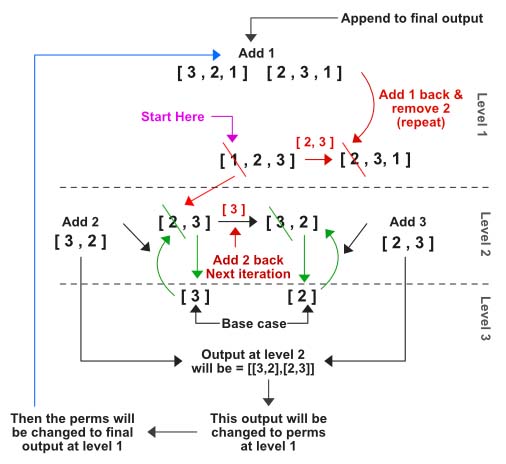
Here is the different way to explain the same algorithm.

Final Code

Here is the full code.

def permutations(nums):
	output = []
  
  if len(nums)==1:
    return [nums.copy()]
  
  for index in range(len(nums)):
    first = nums.pop(0)

    permutation_arr = permutations(nums)
    for perm in permutation_arr:
      perm.append(first)

    output.extend(permutation_arr)
    nums.append(first)
  
  return output