Backtracking - Permutations II

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Medium

DFS, Backtracking, Map

Problem

Given a collection of numbers, nums, that might contain duplicates, return all possible unique permutations in any order.

Example 1:

Input: nums = [1,1,2]
Output:
[[1,1,2],
 [1,2,1],
 [2,1,1]]

Example 2:

Input: nums = [1,2,3]
Output: [[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

Solution

This is very similar to the previous Permutations problem however like we used almost the same solution for Subset II from Subset, we won’t be able to do the same. Here in order to avoid the duplicates, we will transform the input list to a map object and use that to traverse the dfs() for negating sequences.

nums_map=collections.defaultdict(int)
for n in nums:
  nums_map[n]+=1

{
	1: 2, 
	2: 1
}

In the dfs() function, the terminating/base condition is similar to what we have used in the Subset problem. Like in the Subset problem we will define permutation_arr outside, though it can also be passed as an argument in the dfs() function.

permutation_arr = []
output=[]
def dfs():
  if len(permutation_arr) == len(nums):
    output.append(permutation_arr.copy())
    return

Now we will loop through each unique element in the nums_map. If the number in the nums_map is more than 0 then we know we can call dfs() again. The idea is to keep subtracting the value from the nums_map however the loop will only be for len(nums_map.keys()). This will ensure number of unique combinations are equal to number of unique elements in the input nums array.

  for key in nums_map:
    if nums_map[key] >0 :
    ...

Now add each key to the permutation_arr , decrement the counter in the nums_map then run dfs(). Once its completed perform the backtracking.

  for key in nums_map:
    if nums_map[key] >0 :
      permutation_arr.append(key)
      nums_map[key]-=1
    
      dfs()
    
      nums_map[key]+=1
      permutation_arr.pop()

Finally invoke dfs() and return the output.

dfs()
return output

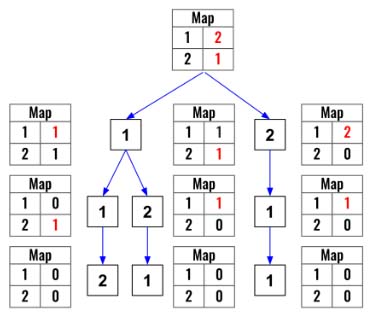
Here is the visualization.

Final Code

Here is the full code.

def permutations_ii(nums):
    output = []
    permutation_arr = []
    nums_map = collections.defaultdict(int)
    for n in nums:
        nums_map[n] += 1

    def dfs():
        if len(permutation_arr) == len(nums):
            output.append(permutation_arr.copy())
            return

        for key in nums_map:
            if nums_map[key] > 0:
                permutation_arr.append(key)
                nums_map[key] -= 1

                dfs()

                nums_map[key] += 1
                permutation_arr.pop()

    dfs()
    return output