Tree - Longest Increasing Path in a Matrix

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

DFS

Problem

Given an m x n integers matrix, return the length of the longest increasing path in matrix.

From each cell, you can either move in four directions: left, right, up, or down. You may not move diagonally or move outside the boundary (i.e., wrap-around is not allowed).

Constraints:

• 0 <= matrix[i][j] <= 231 - 1

Example 1:

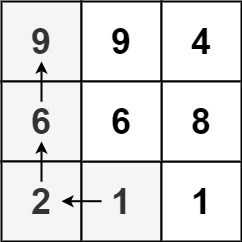
Input: matrix = [[9,9,4],[6,6,8],[2,1,1]]
Output: 4
Explanation: The longest increasing path is [1, 2, 6, 9].

Example 2:

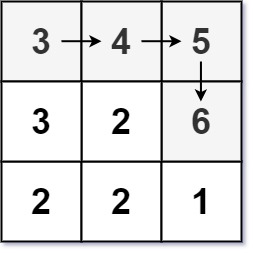
Input: matrix = [[3,4,5],[3,2,6],[2,2,1]]
Output: 4
Explanation: The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.

Example 3:

Input: matrix = [[1]]
Output: 1

Solution

Even though this problem is marked as hard in LeetCode its a simple problem. Let’s break in down in a step by step way. This is a graph traversal problem (like others we have seen) where we need to run dfs() [Not bfs() as we are looking for a single solution from one node] from every cell and find out which path is the largest.

So we need to save the max possible path from every cell. We can definitely use another matrix with same rows and cols to store this value. Later we can find which cell has the max value and just return that. For the Example 1 , it might look like this:

[
  [1,1,1],
  [2,2,2],
  [3,4,2]
]

So we can see the max is 4 which will be returned.

Now instead of creating a new matrix we can reuse our visited variable. Instead of creating a visited set we will create a visited map here.

ROWS, COLS = len(matrix),len(matrix[0])
visited={}

Next step is to write the dfs() for each cell. The dfs function takes the row, col and the previous value to compare as we need to make sure the current cell is greater than previous one, otherwise the dfs() needs to stop.

Start with the boundary conditions. Return 0 if any one the following condition can be met and do not traverse to the neighbors.

def dfs(r, c, prev):
  if r< 0 or c<0 or r==ROWS or c == COLS or matrix[r][c]<=prev:
    return 0

Next, if the matrix[r][c] > prev then traverse all four neighbors and find the which direction provides the max path length.

  max_path_so_far = max(dfs(r-1,c,matrix[r][c]), dfs(r+1,c,matrix[r][c]), dfs(r,c-1,matrix[r][c]),dfs(r,c+1,matrix[r][c]))

In case the matrix[r][c] is the only one which can be traversed, the max_path_so_far above will be 0 returned by the base condition we have written above. For an example, if 9 is being traversed, there is no where else to go since 9 is the highest number hence the max_path_so_far above will be 0.

We need to account for the cell matrix[r][c], so we will increment max_path_so_far by one. This way the visited[(r,c)] for 9 will be 1. Here are the values again.

Now let’s add the max_path_so_far to visited and return max_path_so_far.

  visited[(r,c)]=max_path_so_far
  return max_path_so_far

Now we need to run the dfs for each cell and populate visited map. We will pass -1 as the prev in the beginning as the lowest value can be 0. (Please refer the constraints above)

for r in range(ROWS):
  for c in range(COLS):
    dfs(r,c,-1) 

Finally, return the max value in the visited map.

return max(visited.values())

Logically the above code is going to work fine for smaller matrix, however for larger one its going to show Time Limit Exceeded error. One easy way to solve it is using cache. We can just return the cell max if available from the visited map, we do not have to traverse it anymore. This will save significant time. Let’s add that to the dfs() function before traversing all directions.

  if (r,c) in visited:
    return visited[(r,c)]

Final Code

Here is the full code.

def longest_increasing_path(matrix) -> int:
    ROWS, COLS = len(matrix), len(matrix[0])
    visited = {}

    def dfs(r, c, prev):
        if r < 0 or c < 0 or r == ROWS or c == COLS or matrix[r][c] <= prev:
            return 0
				
        if (r,c) in visited:
          return visited[(r,c)]
        
        max_path_so_far = max(dfs(r-1, c, matrix[r][c]), dfs(r+1, c, matrix[r][c]),
                     dfs(r, c-1, matrix[r][c]), dfs(r, c+1, matrix[r][c]))
        max_path_so_far += 1

        visited[(r, c)] = max_path_so_far
        return max_path_so_far

    for r in range(ROWS):
        for c in range(COLS):
            dfs(r, c, -1)

    return max(visited.values())