Tree - Count Sub Islands

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

DFS

Problem

You are given two m x n binary matrices grid1 and grid2 containing only 0’s (representing water) and 1’s (representing land). An island is a group of 1’s connected 4-directionally (horizontal or vertical). Any cells outside of the grid are considered water cells.

An island in grid2 is considered a sub-island if there is an island in grid1 that contains all the cells that make up this island in grid2. Return the number of islands in grid2 that are considered sub-islands.

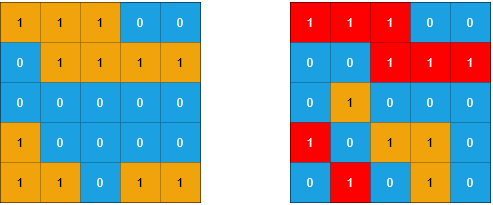
Example 1:

Input: grid1 = [[1,1,1,0,0],
		[0,1,1,1,1],
		[0,0,0,0,0],
		[1,0,0,0,0],
		[1,1,0,1,1]], 
grid2 = [[1,1,1,0,0],
	[0,0,1,1,1],
	[0,1,0,0,0],
	[1,0,1,1,0],
	[0,1,0,1,0]]
	
Output: 3
Explanation: In the picture above, 
the grid on the left is grid1 and 
the grid on the right is grid2.
The 1s colored red in grid2 are those considered
to be part of a sub-island. There are three sub-islands.

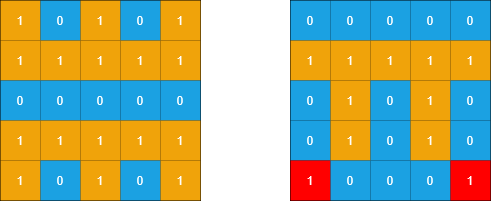
Example 2:

Input: grid1 = [[1,0,1,0,1],
		[1,1,1,1,1],
		[0,0,0,0,0],
		[1,1,1,1,1],
		[1,0,1,0,1]], 
grid2 = [[0,0,0,0,0],
	[1,1,1,1,1],
	[0,1,0,1,0],
	[0,1,0,1,0],
	[1,0,0,0,1]]
	
Output: 2 
Explanation: In the picture above, the grid on 
the left is grid1 and the grid on the right is grid2.
The 1s colored red in grid2 are those considered 
to be part of a sub-island. There are two sub-islands.

Solution

This is not a difficult problem but there is a small trick that needs to be implemented. Let visit step by step process.

First as usual define the two variables we need for the dfs() function.

ROWS, COLS = len(grid2), len(grid2[0])
visited = set()

The dfs() function will return a True or False based on if this is truly a sub-island or not.

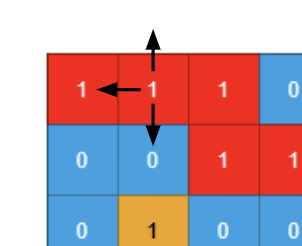
Now inside the dfs() function lets understand the boundary conditions first. We will use the Example 1, and focus on the [0,1] and assume we are traversing this specific cell. The left [0,0] cell is already visited, so we will check for (r,c) in visited which will be True and we will not progress any further by returning from this point.

Next, the top cell [-1,1] is out of bound so we will not progress any further by returning from this point as well.

Finally, bottom cell [1,1] contains 0 (water) so we will not progress any further by returning from this point.

The most important thing to notice that none of the above conditions,

1. Previously visited cell
2. Out of bound cell
3. Cell containing Water

invalidates the current progression of finding sub-islands.They are all valid scenarios where we shouldn’t traverse more, and thats all. So we shall return True whenever any one of the three scenarios occurs.

def dfs(r,c):
	if r < 0 or c < 0 or r == ROWS or c == COLS or (r, c) in visited or grid2[r][c] == 0:
    return True

Now we know we have a cell with value 1, lets first add it to the visited set.

visited.add((r,c))

Now there are 5 separate conditions to validate to make sure this is truly a sub-island.

• The current location/cell in grid1 is also 1.
• The dfs() calls of all 4 surroundings are also either:
  • One of the 3 base conditions and
  • Corresponding cell in grid1 is also 1

Here are the all five conditions. All of them needs to be True for the sub-island to be valid.

if grid1[r][c] == 0:
  current_cell = False
else:
  current_cell=True
  
bottom=dfs(r+1,c)
top=dfs(r-1,c)
right=dfs(r,c+1)
left=dfs(r,c-1)

Now there is one thing in python thats important to know. If there are multiple and then python will start executing from left to right, however if it receives False then it will stop executing the remaining conditions.

Consider following return statement. If in case current_cell is False , then the remaining dfs() functions will not be executed at all.

return current_cell and dfs(r+1,c) and dfs(r-1,c) and ...

In our case, even one of the above 5 conditions returns False, we shall go ahead & add all the cells in the island to the visited set.

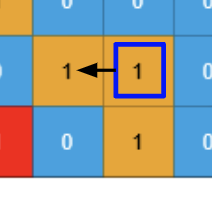
For an example, in Example 1, when we are traversing the cell highlighted below, the matching cell in grid1 is 0, so we know its not a valid sub-island. However we still need to add the left of the cell with value 1 to the visited set, so that we don’t start the dfs() again from that cell. All 3 cells creates one island so we need to initiate dfs() only once.

In order to achieve this, we will be invoking dfs() 4 times and then only returning the final result like below and not like we did above (return current_cell and dfs(r+1,c) and dfs(r-1,c) and ...).

return current_cell and top and bottom and right and left

The only thing left is to invoke dfs() whenever there is an unvisited island.

islant_counter=0
for r in range(ROWS):
  for c in range(COLS):
    if grid2[r][c]==1 and (r,c) not in visited:
      if dfs(r,c):
        islant_counter+=1
        
return islant_counter

Final Code

Here is the full code.

def count_sub_islands(grid1, grid2):
    ROWS, COLS = len(grid2), len(grid2[0])
    visited = set()

    def dfs(r, c):
        if r < 0 or c < 0 or r == ROWS or c == COLS or (r, c) in visited or grid2[r][c] == 0:
            return True

        visited.add((r, c))

        if grid1[r][c] == 0:
            current_cell = False
        else:
            current_cell = True

        bottom = dfs(r+1, c)
        top = dfs(r-1, c)
        right = dfs(r, c+1)
        left = dfs(r, c-1)

        return current_cell and top and bottom and right and left

    islant_counter = 0
    for r in range(ROWS):
        for c in range(COLS):
            if grid2[r][c] == 1 and (r, c) not in visited:
                if dfs(r, c):
                    islant_counter += 1

    return islant_counter