Tree - Network Delay Time

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

Dijkstra’s Algorithm (Graph), BFS, Min-Heap

Problem

You are given a network of n nodes, labeled from 1 to n. You are also given times, a list of travel times as directed edges times[i] = (ui, vi, wi), where ui is the source node, vi is the target node, and wi is the time it takes for a signal to travel from source to target.

We will send a signal from a given node k. Return the minimum time it takes for all the n nodes to receive the signal. If it is impossible for all the n nodes to receive the signal, return -1.

Example 1:

Input: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
Output: 2

Solution

This is the classic Dijkstra’s Algorithm. If you know how to solve it then there is no additional explanation is required.

High Level Explanation

1. Traverse the graph based on current smallest weights using min heap.
2. Do not visit a node if its already visited using the visit set.
3. Add cumulative weight as the key to the min heap.

The first thing we will do it create the edge list (Adjacency Map). This part is very common for most of the graph problem. Loop through each element in times array and append the connected nodes with the edge weights.

def network_delay_time(times,n,k):
  edges = collections.defaultdict(list)
  for u, v, w in times:
    edges[u].append((v,w))

We need to start from the provided node k. Add that manually to the min-heap with weight set to 0 as this will be the starting node.

The weight is the first element in the tuple, hence the heap will be sorted based on the weight by default.This is one of the most important step

  min_heap = [(0,k)]

Create a visited set for avoiding duplicate paths and distance for tracking the last visited node.

  visited = set()
  distance = 0

Next, keep looping until the min_heap is not empty so that we can traverse across the entire directed graph using BFS. During every visit, pop the top element from the min_heap which is the node with min weight.

  while min_heap:
    parent_weight,parent_node = heapq.heappop(min_heap)

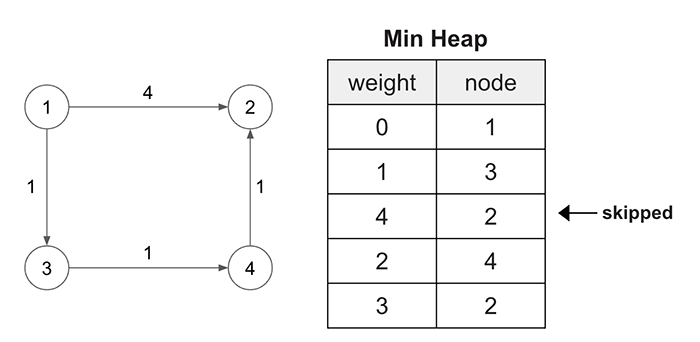
Here is a sample of how the logic is going to workout. We will start from node 1 and traverse through the graph. Notice, the node 2 can be reached in two different ways, however (4,2) entry will be skipped as (3,2) will be popped before it and the node 2 will be marked as visited in the set().

If the popped node is already in the visited set we won’t do anything. Any node with alternative larger cumulative weight will not be processed automatically using the visited set().

    if parent_node in visited:
    	continue

Otherwise add it to the visited set and save the parent_weight . The assumption here is the last visited node will always be farthest away from node k as we are always popping the min weight from the min_heap. This distance will be returned at the end.

This is the extra step added on top of basic Dijkstra's Algorithm with BFS.

This is one of the most important step that you might miss to understand. The distance will be returned at the end, hence the parent_weight must be assigned to it only after the validation that the parent_node is not in the visited set. This way we will know parent_node must be part of the path. Adding this before the previous if will cause issues as visited node’s weights will be returned, which is not desired.

    visited.add(parent_node)
    distance = parent_weight

Now add all the nodes in the min_heap which can be reached from the parent_node.

The last line is the most important where we are appending the parent_weight with the child_weight to get the cumulative weight to reach from node k to the current child_node.

    for child_node, child_weight in edges[parent_node]:
    	if child_node not in visited:
      	heapq.heappush(min_heap, (parent_weight+child_weight,child_node))

Finally, return the distance only if we have visited all the n nodes, else return -1.

  return distance if len(visited) ==n else -1

Final Code

Here is the full code.

def network_delay_time(times, n, k):
    edges = collections.defaultdict(list)
    for u, v, w in times:
        edges[u].append((v, w))

    visited = set()
    distance = 0
    min_heap = [(0, k)]

    while min_heap:
        parent_weight, parent_node = heapq.heappop(min_heap)
        if parent_node in visited:
            continue

        distance = parent_weight
        visited.add(parent_node)

        for child_node, child_weight in edges[parent_node]:
            if child_node not in visited:
                heapq.heappush(
                    min_heap, (parent_weight+child_weight, child_node))

    return distance if len(visited) == n else -1