Backtracking - Generate Parentheses

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

DFS, Backtracking, Stack

Problem

Given n pairs of parentheses, write a function to generate all combinations of well-formed parentheses.

Example 1:

Input: n = 3
Output: ["((()))","(()())","(())()","()(())","()()()"]

Example 2:

Input: n = 1
Output: ["()"]

Solution

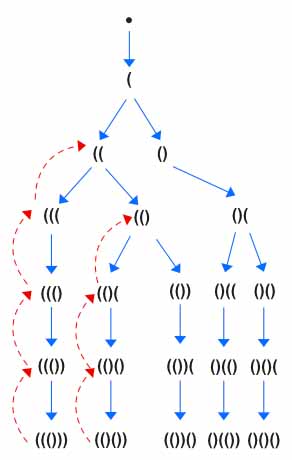
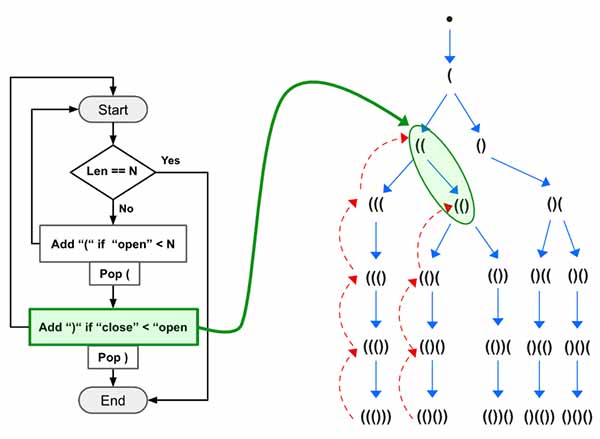
If you have ever solved these types of problem then you know use of stack is very common to keep track of number of Parentheses. Before getting into the logic lets visualize the graph.

Here is the high level idea:

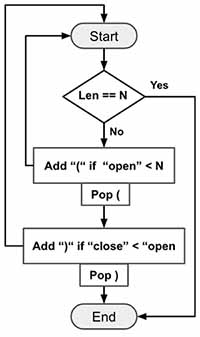
• Use DFS to find various paths.
• Keep adding ( and call dfs() until the number of open parentheses reaches n
• Keep adding ) and call dfs() only if number of close parentheses is less than the open parentheses.

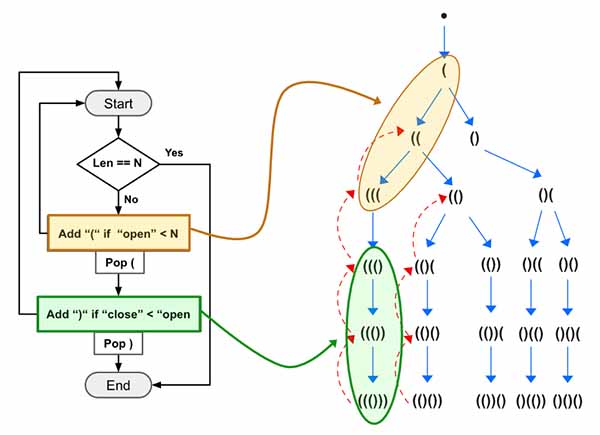
Now let’s go through the Example 1, At first the Yellow box will run 3 times (Yellow Box) and add ((( into the stack. the backtracking (pop()) won’t be executed here. Then on the 4th run, the yellow part won’t be executed as number of open will be equal to N. Now the green box will run 3 times and will produce ((())).

Now the length of the generated sequence will have both open==close==N. So we will add it to the output and return.

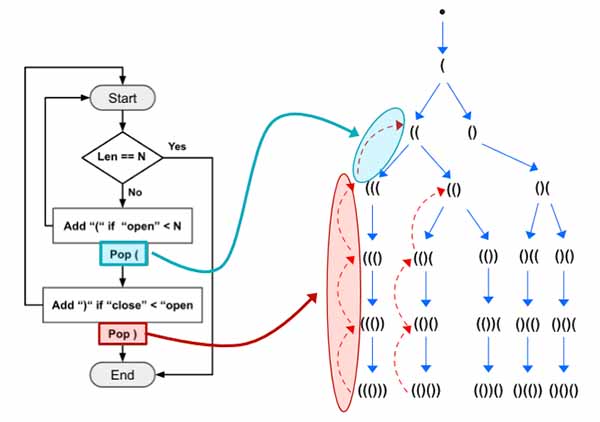
At first the close (red) backtracking logic (pop()) will be executed 3 times. Then the open (blue) backtracking logic (pop()) will be executed only once.

The close logic (green) will be executed again. This will add ) into the stack. Similarly the rest of the program will continue running.

Visualizing the problem helps us to develop the intuition before trying to code it. Now let’s start by defining the variables.

We need an array to store the outputs, we also need a stack. Luckily in python an array can also behave like a stack.So lets define two variables.

output = []
stack = []

Define the dfs() function. We need to keep track of open & close parentheses. So the dfs will take both of them as argument.

def dfs(open_count, close_count):

Define the terminating condition. Whenever the open_count and close_count are equal to n, we know we have a valid sequence.

def dfs(open_count, close_count):
  if open_count == close_count == n:
    output.append("".join(stack))
    return

Now keep adding the open ( parentheses if the open_count < n using dfs(). Increment the open_count by 1 and once done backtrack by popping from the stack.

if open_count < n:
  stack.append("(")
  dfs(open_count+1,close_count)
  stack.pop()

Do the same for the close_count, expect the logic is different. Add close_count only if its < open_count.

if close_count < open_count:
  stack.append(")")
  dfs(open_count,close_count+1)
  stack.pop()

At the end, invoke the dfs() and return output.

dfs(0,0)
return output

Final Code

Here is the full code.

def generate_parentheses(n):
    output = []
    stack = []

    def dfs(open_count, close_count):
        if open_count == close_count == n:
            output.append("".join(stack))
            return

        if open_count < n:
            stack.append("(")
            dfs(open_count+1, close_count)
            stack.pop()

        if close_count < open_count:
            stack.append(")")
            dfs(open_count, close_count+1)
            stack.pop()
    dfs(0, 0)
    return output