Backtracking - Letter Combinations of a Phone Number
All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.
Difficulty : Easy
DFS, Backtracking
Problem
Given a string containing digits from 2-9 inclusive, return all possible letter combinations that the number could represent. Return the answer in any order.
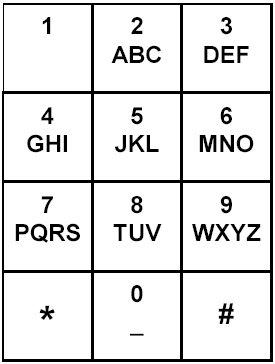
A mapping of digits to letters (just like on the telephone buttons) is given below. Note that 1 does not map to any letters.
Example 1:
1
2
Input: digits = "23"
Output: ["ad","ae","af","bd","be","bf","cd","ce","cf"]
Example 2:
1
2
Input: digits = ""
Output: []
Example 3:
1
2
Input: digits = "2"
Output: ["a","b","c"]
Solution
Let’s define all the dependencies using a map.
1
2
3
4
5
6
7
8
9
10
num2char={
"2": "abc",
"3": "def",
"4": "ghi",
"5": "jkl",
"6": "mno",
"7": "pqrs",
"8": "tuv",
"9": "wxyz",
}
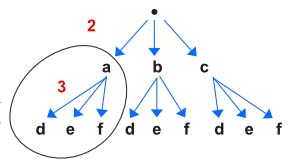
Now build the graph to visualize. We need to traverse top-down.
A dfs() function should be able to solve this easily. The dfs function can take the index of the input nums and at each level we can just pass the prev_chars. Whenever len(prev_chars)==len(nums) we can append it to the output array.
1
2
3
4
def dfs(index,prev_chars):
if len(prev_chars)==len(nums):
output.append(prev_chars)
return
Since at each level there are multiple options, we can loop through each of them and call the dfs() function.
1
2
for c in num2char[nums[index]]:
dfs(index+1,prev_chars+c)
Finally invoke thedfs()
1
2
3
4
if nums:
dfs(0,"")
return output
This is the simple solution which didn’t need backtracking as we know each path would lead to a success. If that wasn’t the case then we should have had implemented the backtracking. Here is an example of how the same solution would work using backtracking.
We increment index and add c to prev_chars. Then after invoking dfs() we again backtrack. As you clearly see this backtracking is unnecessary as each path will lead to a solution.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def dfs(index,prev_chars):
if len(prev_chars)==len(nums):
output.append(prev_chars)
return
for c in num2char[nums[index]]:
prev_chars+=c
index+=1
dfs(i,prev_chars)
#backtracking - not required here
index-=1
prev_chars=prev_chars[:-1]
Final Code
Here is the full code.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def letter_combinations(nums):
output = []
num2char = {
"2": "abc",
"3": "def",
"4": "ghi",
"5": "jkl",
"6": "mno",
"7": "pqrs",
"8": "tuv",
"9": "wxyz",
}
def dfs(index, prev_chars):
if len(prev_chars) == len(nums):
output.append(prev_chars)
return
for c in num2char[nums[index]]:
dfs(index+1, prev_chars+c)
if nums:
dfs(0, "")
return output