Backtracking - Combinations

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

DFS, Backtracking

Problem

Given an integer array nums and an integer k, return true if it is possible to divide this array into k non-empty subsets whose sums are all equal.

Example 1:

Input: nums = [4,3,2,3,5,2,1], k = 4
Output: true
Explanation: It is possible to divide it into 4 subsets (5), (1, 4), (2,3), (2,3) with equal sums.

Example 2:

Input: nums = [1,2,3,4], k = 3
Output: false

Solution

A very simple problem to solve and almost similar to the Find Unique Binary String problem.

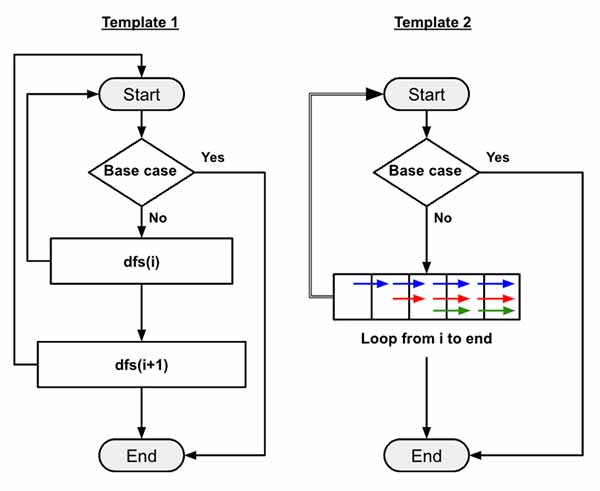
So from every index we need to start a dfs() to create combinations of length k using all 1 to n numbers.

This instantly guides us to use template 2 that we have already discussed here.

Define the output variable.

output = []

Then create the dfs() which will take the index and current path. Whenever the len(path)==k we can append the path to output.

def dfs(index, path):
  if len(path) == k:
    output.append(path.copy())
    return

Now define the for loop to call dfs() recursively. Below for the right boundary, we need to include +1 as the numbers start from 1 and not 0.

  for j in range(index,n+1):
    path.append(j)
    dfs(j+1,path)
    path.pop()

At the end, call dfs() and return output.

dfs(1,[])
return output

Final Code

Here is the full code.

def combine(n, k):
    output = []

    def dfs(index, path):
        if len(path) == k:
            output.append(path.copy())
            return
        for j in range(index, n+1):
            path.append(j)
            dfs(j+1, path)
            path.pop()

    dfs(1, [])
    return output