Tree - Spiral Matrix
All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.
Difficulty : Easy
Divide and Concur, 4 pointers
Problem
Given an m x n matrix, return all elements of the matrix in spiral order.
Example 1:
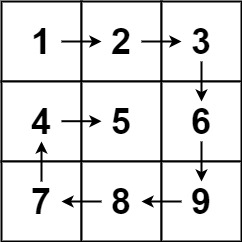
1
2
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]
Example 2:
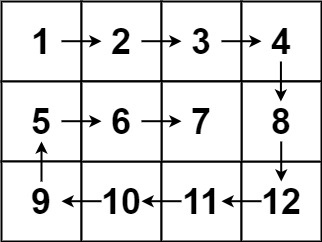
1
2
Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]
Solution
Just like the previous problem (Rotate Image), we need to solve this for one layer. This problem is also very similar. The Rotate Image problem can be technically solved using 2 pointers as top and bottom values will always be same as left and right. However, that is not the case here as we have m x n matrix (not n x n).
- Use 4 pointers (L, R, T, B).
- Once top row is completed update T → T+1
- Once right col is completed update R→ R -1
- Once bottom row is completed update B→ B -1
- Once left col is completed update L→ L -1
- Exit conditions are when
L==R or T==B
As the figure shows, we need to move the 4 pointers until we have completed flatten out one layer. Repeat the same unless the pointers cross over.
Start by defining the pointers.
1
2
3
4
5
6
ROWS, COLS = len(matrix), len(matrix[0])
left, right = 0, COLS
top, bottom = 0 , ROWS
flatten_array=[]
Let’s skip the loop part and find out how to unwrap one layer first. Need to move the left pointer till it reaches the right pointer. Since the left to right was for the top row, we will increment top by 1 as well.
1
2
3
for i in range(left,right):
flatten_array.append(matrix[top][i])
top+=1
Now the right column (blue arrows). Since top is already incremented by 1, we will only capture from 2nd row, which is what we want as well. Also decrement the right pointer.
1
2
3
for i in range(top,bottom):
flatten_array.append(matrix[i][right-1])
right-=1
Similarly, for the last row (Green Arrow), the range() function needs to be in reverse way.
1
2
3
4
for i in range(right-1,left-1,-1):
flatten_array.append(matrix[bottom-1][i])
bottom-=1
Finally, for the left col.
1
2
3
for i in range(bottom-1,top-1,-1):
flatten_array.append(matrix[i][left])
left+=1
Now here is the while loop, very similar to the previous problem.
1
2
while left < right and top < bottom:
...
The above code is going to work fine for input matrix where there is no one dimensional sub matrix that we need to flatten out. However for scenarios as given below, if there are sub-matrix which are one dimensional ([6,7] or [11,12]), the above code is not going to work.
The reason is, left->right will add 6,7 into the flatten_array, which is fine and expected. Then top->bottom loop won’t be executed as by now we already have incremented top by 1. So both top and bottom will have the same value.
However, right->left loop will be executed as right was decremented by 1 however left was not incremented. Since this is 1D matrix (vector) now right->left will add same number into the flatten_array which is wrong.
In case of the 2nd example, the right->left would be fine as they will have the same value. However, the bottom->top will still be executed, which will add extra element in the flatten_array.
In order to overcome this issue, we need to find out if left==right (for 1D row, like in the left example) or top==bottom after left->right and top-bottom. If so then break the while loop as at this point we are done adding all the elements into the flatten_array.
1
2
if left==right or top==bottom:
break
Final Code
Here is the full code.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
def spiral_order(matrix):
ROWS, COLS = len(matrix), len(matrix[0])
left, right = 0, COLS
top, bottom = 0 , ROWS
flatten_array=[]
while left < right and top < bottom:
for i in range(left,right):
flatten_array.append(matrix[top][i])
top+=1
for i in range(top,bottom):
flatten_array.append(matrix[i][right-1])
right-=1
if left==right or top==bottom:
break
for i in range(right-1,left-1,-1):
flatten_array.append(matrix[bottom-1][i])
bottom-=1
for i in range(bottom-1,top-1,-1):
flatten_array.append(matrix[i][left])
left+=1
return flatten_array