Matrices - Rotate Image

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

Divide and Concur, 4 pointers

Problem

You are given an n x n 2D matrix representing an image, rotate the image by 90 degrees (clockwise).

You have to rotate the image in-place, which means you have to modify the input 2D matrix directly. DO NOT allocate another 2D matrix and do the rotation.

Example 1:

Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [[7,4,1],[8,5,2],[9,6,3]]

Example 2:

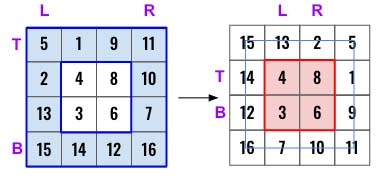
Input: matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
Output: [[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]

Solution

We have to rotate each layers at once and move inward. Refer the fig below, we need to rotate the outer later (in blue) first before rotating the inner layer (red).

Once thats clear, the next important part is use of 4 pointers left, right, top and bottom when trying to rotate the matrix. The exit condition is: whenever left=>right we know there is no inner layer to rotate too. Like in the example above, once the red matrix gets rotated, left will be >= right as after every iteration we will be incrementing left and decrementing right.

We will start with left and right pointer. The top and bottom pointer will be same as left and right, as we have n x n matrix. Here is the structure of the while loop and we will keep moving all the pointers.

left, right = 0, len(matrix)-1
while left < right:
  top, bottom = left,right
  
  # To be implemented
  rotate(left,right,top,bottom)
  
  left+=1
  right-=1

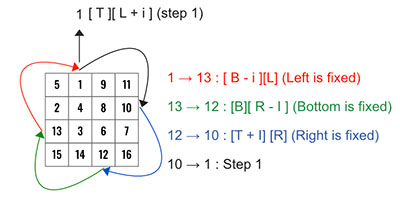
For the rotate() function, let’s visualize the solution first.

• The bottom-left (15) will be assigned to top-left.
• The bottom-right (16) will be assigned to bottom-left.
• The top-right (11) will be assigned to bottom-right.
• Finally, the top-left (5) will be assigned to top-right.

We need to repeat this t times (t is one less than the number of row/col in the layer we are rotating) and every time we need to move the pointers. Let’s create a loop which can do this automatically. We can find t using left and right as t = right -left.

We will be moving left forward and right backward and the different in them is basically t. For the outer layer in the above diagram, t= (3-0) = 3 and for the inner layer its t = (2-1) = 1.

Now let’s write the logic of rotating one element. The generic logic will be top_left_cache = matrix[top][left], however we know that left needs to move forward once the first element is done. So let’s have it incremented by i. i will run from 0 till t. So left+i

top_left_cache = matrix[top][left+i]

Now, the bottom-left (15) will be assigned to top-left. Here left is fixed, but bottom needs to move upward, means it needs to be decremented by i. So bottom-i

matrix[top][left+i] = matrix[bottom-i][left]

Repeat the same for matrix[bottom][right] and ``

matrix[bottom-i][left] = matrix[bottom][right-i]
matrix[bottom][right-i] = matrix[top+i][right]

Finally, resign matrix[top+1][right] from top_left_cache

matrix[top+i][right] = top_left_cache

We can have all these into one function named rotate_one_element

def rotate_one_element(left,right,top,bottom,i):
  top_left_cache = matrix[top][left+i]
  
  matrix[top][left+i] = matrix[bottom-i][left]
  matrix[bottom-i][left] = matrix[bottom][right-i]
	matrix[bottom][right-i] = matrix[top+i][right]
  matrix[top+i][right] = top_left_cache

Here is another visualization for the 2nd element.

Add a for loop inside rotate() which will call rotate_one_element().

def rotate(left,right,top,bottom):
  for i in range(right-left):
    rotate_one_element(left,right,top,bottom,i)

Final Code

Here is the full code.

def rotate_image(matrix):
  def rotate_one_element(left,right,top,bottom,i):
    top_left_cache = matrix[top][left+i]

    matrix[top][left+i] = matrix[bottom-i][left]
    matrix[bottom-i][left] = matrix[bottom][right-i]
    matrix[bottom][right-i] = matrix[top+i][right]
    matrix[top+i][right] = top_left_cache

  def rotate(left,right,top,bottom):
    for i in range(right-left):
      rotate_one_element(left,right,top,bottom,i)
    
  left, right = 0, len(matrix)-1
  
  while left < right:
    top, bottom = left,right

    rotate(left,right,top,bottom)

    left+=1
    right-=1