Tree - Walls and Gates

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

Multi-Source BFS

Problem

You are given a m x n 2D grid initialized with these three possible values.

1. -1 - A wall or an obstacle.
2. 0 - A gate.
3. INF - Infinity means an empty room. We use the value 231 - 1 = 2147483647 to represent INF as you may assume that the distance to a gate is less than 2147483647.

Fill each empty room with the distance to its nearest gate. If it is impossible to reach a gate, it should be filled with INF.

Example 1:

Given the 2D grid:

INF  -1  0  INF
INF INF INF  -1
INF  -1 INF  -1
  0  -1 INF INF

After running your function, the 2D grid should be:

  3  -1   0   1
  2   2   1  -1
  1  -1   2  -1
  0  -1   3   4

Solution

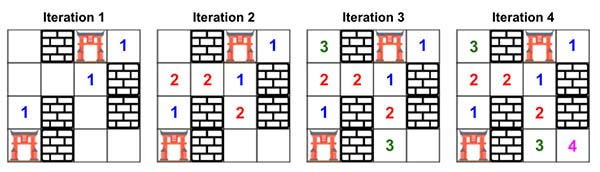
Here is a simpler diagram to understand. This is a Multi-Source BFS problem, means initially we are going to have more than one root in the queue and run BFS for all of them.

Start by creating the needed variables.

ROWS, COLS = len(rooms), len(rooms[0])
visited=set()
queue = collections.deque()
directions = [[1,0],[0,1],[0,-1],[-1,0]]

Next step would be to identify all the gates and push them to both the visited set and the queue to start with.

for r in range(ROWS):
  for c in range(COLS):
    if rooms[r][c]==0:
      visited.add((r,c))
      queue.append([r,c])
      

We will keep tracking the cost using the distance variable. We just need one distance as in every iteration we will traverse equal distance from each source. Here is the diagram.

distance=0

Process each node in the queue, set the current distance as the cell value, traverse the neighbors and finally increment the distance.

while queue:
  for _ in range(len(queue)):
    r,c = queue.popleft()
    rooms[r][c] = distance
    for dr,dc in directions:
      nei_r, nei_c = r + dr, c + dc
      if nei_r < 0 or nei_c < 0 or nei_r == ROWS or nei_c == COLS or (nei_r, nei_c) in visited or rooms[nei_r][nei_c] == -1:
        continue
      
      queue.append([nei_r, nei_c])
      visited.add((nei_r, nei_c))
      
  distance+=1

Final Code

Here is the full code.

def walls_and_gate(rooms):
    ROWS, COLS = len(rooms), len(rooms[0])
    visited = set()
    queue = collections.deque()
    directions = [[1, 0], [0, 1], [0, -1], [-1, 0]]
    for r in range(ROWS):
        for c in range(COLS):
            if rooms[r][c] == 0:
                visited.add((r, c))
                queue.append([r, c])

    distance = 0
    while queue:
        for _ in range(len(queue)):
            r, c = queue.popleft()
            rooms[r][c] = distance
            for dr, dc in directions:
                nei_r, nei_c = r + dr, c + dc
                if nei_r < 0 or nei_c < 0 or nei_r == ROWS or nei_c == COLS or (nei_r, nei_c) in visited or rooms[nei_r][nei_c] == -1:
                    continue

                queue.append([nei_r, nei_c])
                visited.add((nei_r, nei_c))

        distance += 1
    return rooms

[
	[3, -1, 0, 1], 
	[2, 2, 1, -1], 
	[1, -1, 2, -1], 
	[0, -1, 3, 4]
]

Alternative solution

As you might have seen in other graph problem, this can also be solve by adding visited after popping the node. For more details please refer here.

def walls_and_gate(rooms):
    ROWS, COLS = len(rooms), len(rooms[0])
    visited = set()
    queue = collections.deque()
    directions = [[1, 0], [0, 1], [0, -1], [-1, 0]]
    for r in range(ROWS):
        for c in range(COLS):
            if rooms[r][c] == 0:
              	# Removed this
                # visited.add((r, c))
                queue.append([r, c])

    distance = 0
    while queue:
        for _ in range(len(queue)):
            r, c = queue.popleft()
            
            # Added this
            if (r, c) in visited:
                continue
            visited.add((r, c))
            
            
            rooms[r][c] = distance
            
            for dr, dc in directions:
                nei_r, nei_c = r + dr, c + dc
                if nei_r < 0 or nei_c < 0 or nei_r == ROWS or nei_c == COLS or (nei_r, nei_c) in visited or rooms[nei_r][nei_c] == -1:
                    continue

                queue.append([nei_r, nei_c])
                # visited.add((nei_r, nei_c))

        distance += 1
    return rooms