Tree - Reorder Routes to Lead to City Zero

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

DFS

Problem

There are n cities numbered from 0 to n - 1 and n - 1 roads such that there is only one way to travel between two different cities (this network form a tree). Last year, The ministry of transport decided to orient the roads in one direction because they are too narrow.

Roads are represented by connections where connections[i] = [ai, bi] represents a road from city ai to city bi. This year, there will be a big event in the capital (city 0), and many people want to travel to this city. Your task consists of reorienting some roads such that each city can visit the city 0. Return the minimum number of edges changed. It’s guaranteed that each city can reach city 0 after reorder.

Example 1:

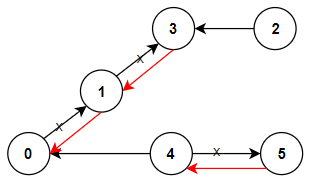
Input: n = 6, connections = [[0,1],[1,3],[2,3],[4,0],[4,5]]
Output: 3
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Example 2:

Input: n = 5, connections = [[1,0],[1,2],[3,2],[3,4]]
Output: 2
Explanation: Change the direction of edges show in red such that each node can reach the node 0 (capital).

Example 3:

Input: n = 3, connections = [[1,0],[2,0]]
Output: 0

Solution

This is a fairly easy solution using either dfs() or bfs(). We have the current routes as given in connections array. We can build a bi-directional graph and traverse through it, then every time we find a node which is not visited yet we find if the route is present in the connections array otherwise we just increment change_needed.

Build the adjacency list first. Remember we need to have it bi-directional, so that we can reach every node.

adjacency_list = collections.defaultdict(list)
for start, end in connections:
  adjacency_list[start].append(end)
  adjacency_list[end].append(start)

Since we are already in city 0, let’s add that to the visited set.

visited=set([0])

Create a variable to count the changes needed.

change_needed = 0

Now define the dfs() function. It will take the node as city. We will just traverse through each of its neighbors and find out if the route already exists, if not increment change_needed by 1.

def dfs(city):
  for neighbor in adjacency_list[city]:
    if neighbor not in visited:
      if [neighbor, city] not in connections:
        change_needed+=1
      
      visited.add(neighbor)
      dfs(neighbor)

Call dfs() by passing the city 0 then return change_needed

dfs(0)
return change_needed

Final Code

The above code will work fine when tested, however this will fail in LeetCode. The main reason is the use of list for lookup. We need to change to be a map for the code to work on Leetcode.

Here is the full code.

def min_reorder(connections):
  current_routes={}
  adjacency_list = collection.defaultdict(list)
  for start, end in connections:
    # Populating the current_routes map 
    current_routes[(start,end)]=True
    
    adjacency_list[start].append(end)
    adjacency_list[end].append(start)
  
  visited=set([0])
  change_needed = 0
  
  def dfs(city):
    nonlocal change_needed
    for neighbor in adjacency_list[city]:
      if neighbor not in visited:
        if (neighbor, city) not in current_routes:
          change_needed+=1

        visited.add(neighbor)
        dfs(neighbor)  
        
	dfs(0)
	return change_needed