Post

Tree - Course Schedule

Posted
By Abhisek Jana 9 min read

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Medium

Backtracking, DFS

Problem

There are a total of numCourses courses you have to take, labeled from 0 to numCourses - 1. You are given an array prerequisites where prerequisites[i] = [ai, bi] indicates that you must take course bi first if you want to take course ai.

  • For example, the pair [0, 1], indicates that to take course 0 you have to first take course 1.

Return true if you can finish all courses. Otherwise, return false.

Example 1:

1
2
3
4

Input: numCourses = 2, prerequisites = [[1,0]]
Output: true
Explanation: There are a total of 2 courses to take. 
To take course 1 you should have finished course 0. So it is possible.

Example 2:

1
2
3
4

Input: numCourses = 2, prerequisites = [[1,0],[0,1]]
Output: false
Explanation: There are a total of 2 courses to take. 
To take course 1 you should have finished course 0, and to take course 0 you should also have finished course 1. So it is impossible.

Solution

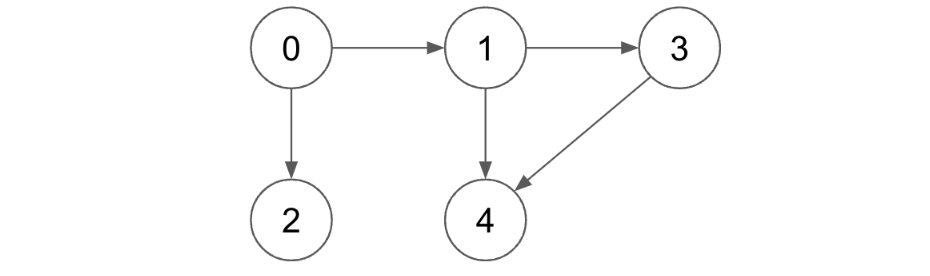
Before going into the solution, let’s visualize a problem. Here is our input:

  • Input : [ [ 0, 1 ] , [ 0, 2 ] , [ 1, 3 ] , [ 1, 4 ] , [ 3, 4 ] ]
  • Output : True

image-20240422111703912

High Level Idea

  1. Very simple and basic DFS problem with Backtracking.
  2. The adjacency map should be able to help to make sure all dependencies can be traversed.
  3. Use visited set() to track cycles.
  4. Return false only when cycle is detected :fire:

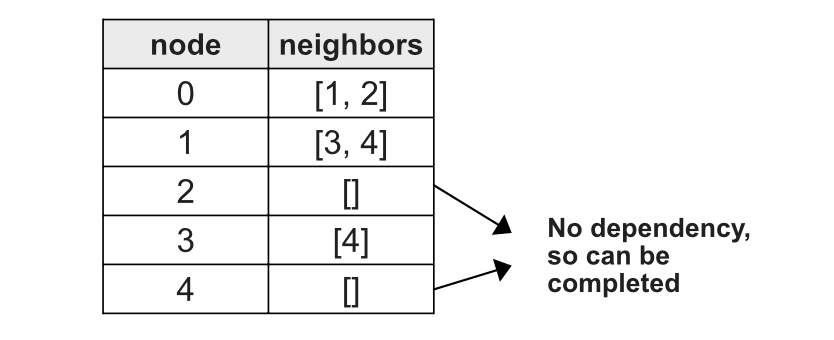
Start by creating the adjacency list.

1
2
3
4

#def can_finish(num_courses, prerequisites)
adjacency_list = collection.defaultdict(list)
for course, prerequisite in prerequisites:
  adjacency_list[course].append(prerequisite)

Define visited set.

1

visited = set()

The idea is to traverse through all the nodes ( 0 to n-1 ) and make sure we can visit all of them. Since the graph can be disjoint we need to run the dfs() starting from all the nodes. If at anytime the dfs() returns False we can just return False and not keep going through running all the nodes.

1
2
3

for course in range(num_courses):
  if not dfs(course):
    return False

In the dfs() function return False if a cycle is detected.

1
2
3

def dfs(course):
  if course in visited:
    return False

Now if there is no prerequisites for a course, we can return True. Like in case of 2 and 4

image-20240422124228637

1
2

  if adjacency_list[course]=[]:
    return True

There are two scenarios in which we can return True, the first one we saw above where the prerequisites are empty in the adjacency_list. The second scenario is when all the prerequisites of the current course is traversed and no cycle is detected (None of the prerequisites courses returned False).

Let’s code for this 2nd scenario. Also, if anytime any of the dfs() returns False (a False is returned only if cycle is detected) we can straightway return False.

1
2
3
4

  for prerequisite in adjacency_list[course]:
    if not dfs(prerequisite):
      return False
  return True

Here is the full code so far. Please take a look and make sure you understand fully as we will be adding some additional lines.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

def can_finish(num_courses, prerequisites):
  adjacency_list = collections.defaultdict(list)
  for course, prerequisite in prerequisites:
    adjacency_list[course].append(prerequisite)
  
  visited = set()
  
  def dfs(course):
    if course in visited:
      return False
    if adjacency_list[course]==[]:
      return True
    visited.add(course)
    
    for prerequisite in adjacency_list[course]:
      if not dfs(prerequisite):
        return False
    return True
  
  for course in range(num_courses):
    if not dfs(course):
      return False
    
  return True

There is two problems with the above code.

1. False Cycle Detection

It’s very important to understand why the above code won’t work and how to make it work. Consider the below example.

  • We will start with 0 which does not have any dependency.
  • Process 1. 1 is dependent on 4. Once we process dfs(1), the visited set will have value 1.
  • Now process 2, similar to 1, once dfs(2) is processed the visited set will have value 1, 2.
  • Now once we start with dfs(3), we will start processing its prerequisite and immediately encounter 1 or 2 in the visited set. This will result in cycle detection and return False, which is inaccurate.
flowchart LR
	0((0))
	1((1))-->4((4))
	2((2))-->4((4))
	3((3))-->1((1))
	3((3))-->2((2))

We might think one way to mitigate is reseting the visited set before line 21 where we call dfs() for each course.

1
2
3
4

for course in range(num_courses):
  	visited = set()
    if not dfs(course):
      return False

It will work for this particular graph, however let’s look at another example. This is a test case in LeetCode.

  • Input : [[1,0],[0,3],[0,2],[3,2],[2,5],[4,5],[5,6],[2,4], num_courses = 7
  • Output : True
flowchart LR
	1((1))-->0((0))
	0((0))-->3((3))
	0((0))-->2((2))
	3((3))-->2((2))
	2((2))-->4((4))
	2((2))-->5((5))
	4((4))-->5((5))
	5((5))-->6((6))
  • We start with visiting 0. The visited set has 0.
  • Then try to process 3 as we have [0,3] before [0,2] in the input given.
  • 3’s prerequisite is 2. So start with 2 which also has more prerequisite. The visited set becomes 0, 2, 3.
  • Now since [2,5] is before [2,4] we visit 5 and then visit 6. The visited set is now 0, 2, 3, 5
  • Now comes [2,4] :fire:, so we run dfs(4), since 4 has prerequisites, we add 4 to visited and start with dfs(5).
  • Here is the problem, the visited already has 5, as we have already processed 5. This detects a false cycle and returns False.

The way to solve this problem is backtracking. Every time all it’s prerequisite have been processed, we need to remove it from the visited set. This way when we visit 5, the visit set does not have 5 as it was removed. So we don’t return False.

1
2
3
4

# remove course from visited before
# returning True at the end
visited.remove(course)
return True

2. Output Limit Exceeded

Logically everything we have done is enough, it will run file in your local. However the above code will fail due to Output Limit Exceeded in LeetCode. One easy way to optimize it to remove the prerequisite of a course after we know all the prerequisites of that course can be completed.

Let’s add some print statements.

1
2
3
4
5
6

def dfs(course):
    print("visiting ->",course)
    if course in visited:
			...
    visited.add(course)
    print(visited)

Here is the log when we visit a node. As you see we are visiting the same nodes even when we know their prerequisites can be fulfilled.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81

visiting -> 0
{0}
visiting -> 3
{0, 3}
visiting -> 2
{0, 2, 3}
visiting -> 5
{0, 2, 3, 5}
visiting -> 6
visiting -> 4
{0, 2, 3, 4}
visiting -> 5
{0, 2, 3, 4, 5}
visiting -> 6
visiting -> 2
{0, 2}
visiting -> 5
{0, 2, 5}
visiting -> 6
visiting -> 4
{0, 2, 4}
visiting -> 5
{0, 2, 4, 5}
visiting -> 6
visiting -> 1
{1}
visiting -> 0
{1, 0}
visiting -> 3
{1, 3, 0}
visiting -> 2
{1, 2, 3, 0}
visiting -> 5
{1, 2, 3, 0, 5}
visiting -> 6
visiting -> 4
{1, 2, 3, 0, 4}
visiting -> 5
{1, 2, 3, 0, 4, 5}
visiting -> 6
visiting -> 2
{1, 0, 2}
visiting -> 5
{1, 0, 5, 2}
visiting -> 6
visiting -> 4
{1, 0, 4, 2}
visiting -> 5
{1, 5, 0, 4, 2}
visiting -> 6
visiting -> 2
{2}
visiting -> 5
{5, 2}
visiting -> 6
visiting -> 4
{4, 2}
visiting -> 5
{5, 4, 2}
visiting -> 6
visiting -> 3
{3}
visiting -> 2
{2, 3}
visiting -> 5
{5, 2, 3}
visiting -> 6
visiting -> 4
{4, 2, 3}
visiting -> 5
{5, 4, 2, 3}
visiting -> 6
visiting -> 4
{4}
visiting -> 5
{5, 4}
visiting -> 6
visiting -> 5
{5}
visiting -> 6
visiting -> 6

So whenever a course’s prerequisites can be completed set the prerequisite of that course to be empty. This way we can avoid multiple round trips and traverse one node (course) just once.

1
2
3
4
5
6

visited.remove(course)
# set the prerequisite to []
# at the end when all of them
# can be reached without any cycle.
adjacency_list[course] = []
return True

Here is the same log after adding this code.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

visiting -> 0
{0}
visiting -> 3
{0, 3}
visiting -> 2
{0, 2, 3}
visiting -> 5
{0, 2, 3, 5}
visiting -> 6
visiting -> 4
{0, 2, 3, 4}
visiting -> 5
visiting -> 2
visiting -> 1
{1}
visiting -> 0
visiting -> 2
visiting -> 3
visiting -> 4
visiting -> 5
visiting -> 6

Here is the code to visualize at once for reference (the variable names might be different).

image-20240422150120847

Final Code

Here is the full code.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

def can_finish(num_courses, prerequisites):
    adjacency_list = collections.defaultdict(list)
    for course, prerequisite in prerequisites:
        adjacency_list[course].append(prerequisite)

    visited = set()

    def dfs(course):
        if course in visited:
            return False

        if adjacency_list[course] == []:
            return True

        visited.add(course)

        for prerequisite in adjacency_list[course]:
            if not dfs(prerequisite):
                return False

        visited.remove(course)
        adjacency_list[course] = []
        return True

    for course in range(num_courses):
        if not dfs(course):
            return False

    return True
algorithm, graph
datastructure
This post is licensed under CC BY 4.0 by the author.