Backtracking - Word Search II

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

DFS, Backtracking, Tries

Problem

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Example 1:

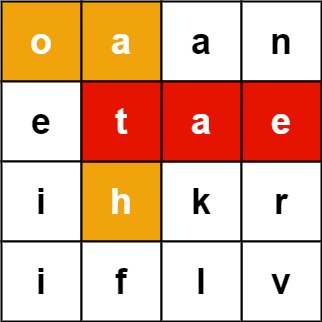
Input: board = [["o","a","a","n"],["e","t","a","e"],["i","h","k","r"],["i","f","l","v"]], words = ["oath","pea","eat","rain"]
Output: ["eat","oath"]

Example 2:

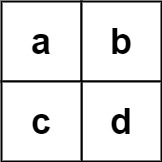
Input: board = [["a","b"],["c","d"]], words = ["abcb"]
Output: []

Solution

This is almost similar as Word Search, however need to search multiple words. Whenever there is a requirement for multiple word search, Tries will be the first algorithm to approach for.

The idea here is a bit different than the last problem. In the last problem we were keeping track of the index which would tell us if we shall traverse more or a word has already been found.

However, here multiple words can start from the same cell and we need to find all of them. So we can’t use the index. Here, we can focus on the current char in the board at location [row][col] and the word it makes by appending it to the existing char-sequence so far traversed. This tell us that we need to pass the current_word instead of the index as one of the argument to the dfs() function.

We will also traverse the Trie simultaneously using the char present in [row][col] . Now, once we know the updated current_word we can see if that word exists in the Trie. If it does then we can add it to the output.

At this point even if we have found one word, does not mean we can return as there might be other words using the same sequence of char as prefix. So we keep traversing in all four direction by pass the current Trie node and current_word.

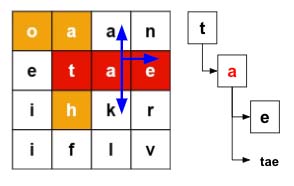
So if a word starts somewhere in-between, we won’t be looking for it just yet. When we start from that cell we will look for that word. For an example, even if [1][1] has a new starting word tae, we won’t be looking for tae unless we start our dfs(1,1) from that cell.

Let’s start coding and see how all this aligns.

Here is the code for the Tries. I am not going to detail, by now you should be knowing enough about Tries to understand the code below.

class TrieNode:
  def __init__(self):
    self.children={}
    self.is_word = False

  def add(self,word):
    node = self
    for char in word:
      if char not in node.children:
        node.children[char]=TrieNode()
      node = node.children[char]
    node.is_word=True

Now the very first step is to add all the words into the Trie.

root = TrieNode()
for word in words:
  root.add(word)

In the previous problem, we returned whenever the word was found, however in this problem since the are multiple words to find, we need to add all identified words in an array. So need another additional output set() to be created. We will use set here as we need to return all unique words and not duplicates.

ROWS, COLS = len(board), len(board[0])
path_visited = set()
output = set()

Similar to the last problem, we need to run dfs() at every cell of the board. We are going to pass the Trie as an additional argument to the dfs() function.Initially we will pass the root, however as we traverse we will traverse through the Trie nodes as well. We will pass the current_word as an empty string as we have not started traversing yet.

for row in range(ROWS):
  for col in range(COLS):
    dfs(row, col, root, '')

Now, the main part of the problem is the dfs() function. As discussed earlier, the dfs() function will take four arguments. Here we are going to focus on the terminating/base condition.

We are going to use the first two conditions from previous problem, however modify the 3rd. Make sure the cell is

• not outside of the boundary conditions and
• not visited and
• the char in the cell is present in the current TrieNode.

Otherwise just return since this indicates there is no possible solution in this path to explore.

def dfs(row, col, trie_node, current_word):
  if row < 0 or col < 0 or row == ROWS or col == COLS or (row,col) in path_visited or board[row][col] not in trie_node.children:
    return

If there are paths forward, lets first add the current location to the path_visited.

  path_visited.add((row,col))

We know that the current char in location [row][col] exists in the TrieNode. Let’s traverse and get that next.

  trie_node = trie_node.children[board[row][col]]

Now construct the new word.

  current_word+=board[row][col]

Add the current_word to output is the is_word flag is True in TrieNode.

  if trie_node.is_word:
    output.add(current_word)

We can’t stop traversing even though we have found one word. Let’s recursively call dfs() to explore all sides. Pass the new TrieNode and updated current_word.

  dfs(row+1,col,trie_node,current_word)
  dfs(row-1,col,trie_node,current_word)
  dfs(row,col+1,trie_node,current_word)
  dfs(row,col-1,trie_node,current_word)

Once traversing is complete, we need to backtrack to make sure to remove the entry from the path_visited

   path_visited.remove((row,col))

That’s all needed for the dfs() function. Now just call return the output as a list.

return list(output)

Final Code

Here is the full code.

class TrieNode:
    def __init__(self):
        self.children = {}
        self.is_word = False

    def add(self, word):
        node = self
        for char in word:
            if char not in node.children:
                node.children[char] = TrieNode()
            node = node.children[char]
        node.is_word = True


def word_search_ii(board, words):
    root = TrieNode()
    for word in words:
        root.add(word)

    ROWS, COLS = len(board), len(board[0])
    path_visited = set()
    output = set()

    def dfs(row, col, trie_node, current_word):
        if row < 0 or col < 0 or row == ROWS or col == COLS or (row, col) in path_visited or board[row][col] not in trie_node.children:
            return
        path_visited.add((row, col))
        trie_node = trie_node.children[board[row][col]]
        current_word += board[row][col]
        if trie_node.is_word:
            output.add(current_word)

        dfs(row+1, col, trie_node, current_word)
        dfs(row-1, col, trie_node, current_word)
        dfs(row, col+1, trie_node, current_word)
        dfs(row, col-1, trie_node, current_word)

        path_visited.remove((row, col))

    for row in range(ROWS):
        for col in range(COLS):
            dfs(row, col, root, '')

    return list(output)