Backtracking - Combinations

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

DFS, Backtracking

Problem

Given two integers n and k, return all possible combinations of k numbers chosen from the range [1, n].

You may return the answer in any order.

Example 1:

Input: n = 4, k = 2
Output: [[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
Explanation: There are 4 choose 2 = 6 total combinations.
Note that combinations are unordered, i.e., [1,2] and [2,1] are considered to be the same combination.

Example 2:

Input: n = 1, k = 1
Output: [[1]]
Explanation: There is 1 choose 1 = 1 total combination.

Solution

The problem is very similar to Combination Sum II however the difference is that we need to find k equal number of combinations and not less. Also in Combination Sum II, we can use one number again in a different combination, but here one number can only be used only once.

So this tells us that,

• We need to keep track of which number is already used and not to use that again (unless we backtrack). In the Combination Sum I & II, we had to keep track of the path only for one combination. However here it needs to be persisted across all traversals.

  used=[False] * len(nums)
  

• Once we identify a solution path_sum==target, we need to run dfs() again by decrementing k. Then when k==0, we can return True

  def dfs(index, path_sum, k):
    if k == 0:
      return True
    
    if path_sum==target:
      return dfs(0,0, k-1)
  

As we discuss in detail, this problem has similarities to the N-Queens problem as well.

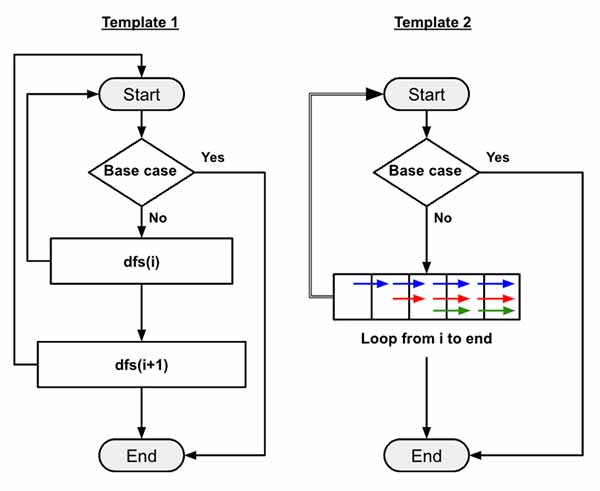
Now, here also we will implement using template 2 that we have already discussed here.

The first thing to do is to find the target. Also define the used array for keeping track of the used numbers.

target = sum(nums) //k
used=[False] * len(nums)

As discussed earlier, the dfs() will take three arguments, index, path_sum & k. Also define the conditions we have created earlier.

def dfs(index, path_sum, k):
  if k == 0:
    return True

  if path_sum==target:
    return dfs(0,0, k-1)

Now as per the template 2, we will use a for loop till end of the nums array from current index. We have the condition to make sure current number is not used and the path_sum+nums[j] <= target. Then set the used[j]=True, run the dfs() function.

If the dfs() returns True, return True immediately. The dfs() will return True only if if k == 0 and this will be True only if dfs(0,0, k-1) runs k-1 times.

Finally backtrack by setting used[j]=False

for j in range(index, len(nums)):
  if not used[j] and path_sum+nums[j] <= target:
    used[j]=True
    if dfs(j+1,path_sum+nums[j],k):
      return True
    used[j]=False
  
  return False
    

Finally, just invoke & return dfs() .

Final Code

Here is the full code.

def can_partition_k_subsets(nums, k):        
    
    target = sum(nums) //k
    used=[False] * len(nums)

    def dfs(index, path_sum, k):
        if k == 0:
            return True

        if path_sum==target:
            return dfs(0,0, k-1)

        for j in range(index, len(nums)):
            if used[j]==False and path_sum+nums[j] <= target:
                used[j]=True
                if dfs(j,path_sum+nums[j],k):
                    return True
                used[j]=False
        return False
    return dfs(0,0,k)