Backtracking - Combination Sum

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

DFS, Backtracking

Problem

Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.

The same number may be chosen from candidates an unlimited number of times. Two combinations are unique if the frequency of at least one of the chosen numbers is different.

The test cases are generated such that the number of unique combinations that sum up to target is less than 150 combinations for the given input.

Example 1:

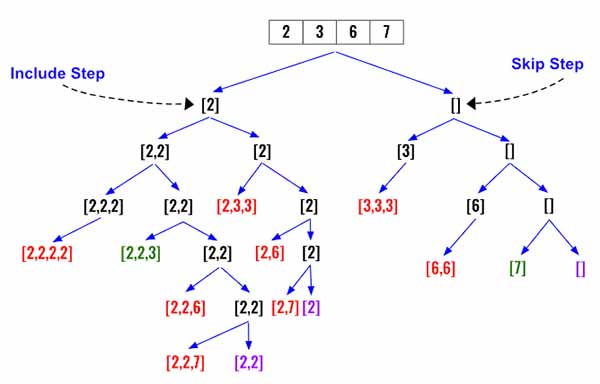
Input: candidates = [2,3,6,7], target = 7
Output: [[2,2,3],[7]]
Explanation:
2 and 3 are candidates, and 2 + 2 + 3 = 7. Note that 2 can be used multiple times.
7 is a candidate, and 7 = 7.
These are the only two combinations.

Example 2:

Input: candidates = [2,3,5], target = 8
Output: [[2,2,2,2],[2,3,3],[3,5]]

Example 3:

Input: candidates = [2], target = 1
Output: []

Solution

I will provide two templates for solving problem like this. However let’s visualize the problem first. Every step of the way we have a decision to make. (1) whether to include current number at index i or (2) not include it and move to next number at i+1.

In the below diagram it’s defined as include step and skip step.

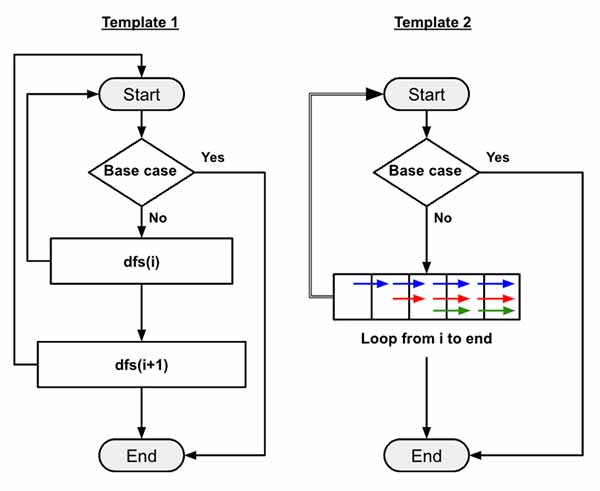
Now to solve problem like this we can follow two separate templates.

• In the template 1, we simulate traversing the array using two recursive calls from each dfs() function. One for current index and another for the next index.
• In template 2, we use a loop to traverse the array recursively for each index position starting from current position.

Basic Structure

Before implementing each solutions, let’s build the basic structure of the code, which is not going to change. We would need one variables for the output to return. The dfs() function takes 3 parameters :

• The index location for traversing
• The path to return to.
• The curr_sum whenever need to determine base case.

output = []

def dfs(index, path, curr_sum):

Lets also define the terminating condition when the path can be added to the output.

def dfs(index, path, curr_sum):
  if curr_sum == target:
    output.append(path.copy())
    return

We will skip the internal logic and finally call the dfs() and return the output.

output = []

def dfs(index, path, curr_sum):
  if curr_sum == target:
    output.append(path.copy())
    return
  
  # Traversal logic goes here
  
def(0,[],0)
return output

Implement using Template 1

When using template 1, we can’t keep incrementing the index so we need to check for boundary condition. We shouldn’t traverse further if any one of the following is True.

if index == len(candidates) or curr_sum > target:
  return

Now it’s time to follow the building blocks of template 1. Here is the dfs(i) call where we first update path and add pass the same index to dfs(). Once done we will pop() back the latest so that we now have the original path to try the next index.

path.append(candidates[index])
dfs(index,path,curr_sum+candidates[index])
path.pop()

Increase the index and call the dfs() using existing path and curr_sum

dfs(index+1,path,curr_sum)

Thats all needed for implementing using template 1.

Implement using Template 2

I feel this implementation is very easy to implement using the Template 2. We need to traverser using a loop till end of the candidates array starting from current index and call dfs() only if the curr_sum+candidates[j]<=target.

Append candidates[j] to current path, call the dfs() and then backtrack path.

for j in range(index,len(candidates)):
  if curr_sum+candidates[j]<=target:
    path.append(candidates[j])
    dfs(j,path,curr_sum+candidates[j])
    path.pop()

Final Code

Here is the full code.

def combinationSum(candidates, target):

    output = []

    def dfs(index, path, curr_sum):
        if curr_sum == target:
            output.append(path.copy())
            return

        '''
        # Using Template 2

        for j in range(index,len(candidates)):
            if curr_sum+candidates[j]<=target:
                path.append(candidates[j])
                dfs(j,path,curr_sum+candidates[j])
                path.pop()
        '''
				
        # Using Template 1
        if index == len(candidates) or curr_sum > target:
            return

        path.append(candidates[index])
        dfs(index, path, curr_sum+candidates[index])
        path.pop()

        dfs(index+1, path, curr_sum)

    dfs(0, [], 0)

    return output