Others - Maximum Product Subarray
All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.
Difficulty : Easy
DP
Problem
Given an integer array nums, find a subarray that has the largest product, and return the product.
The test cases are generated so that the answer will fit in a 32-bit integer.
Example 1:
1
2
3
Input: nums = [2,3,-2,4]
Output: 6
Explanation: [2,3] has the largest product 6.
Example 2:
1
2
3
Input: nums = [-2,0,-1]
Output: 0
Explanation: The result cannot be 2, because [-2,-1] is not a subarray.
Solution
It’s evident that we can solve the problem just by traversing the array one time, but the only problem is the - sign which will shift the result. The - sign will reverse the result, that is, it will change the largest product to smallest one and the smallest one to largest one. Since we won’t have any control over it, why don’t we track both and finally find out the max one.
So let’s create two variables smallest and largest. We need to set them to 1 and not 0 since we are working with product here.
1
smallest, largest = 1, 1
We also need to keep track of the largest at every iteration as in case there is only one negative number then at the end of the loop the largest value may not be largest. Try to solve [2,3,-2,4] and you will see at the end the largest is 4, however the correct result is 2 x 3 = 6 and not 4.
The other important trick to understand which value to initialize this with ? We know that the nums array can have any number, positives or negatives.
Say there is just one number and that is negative [-5] then the max_product must be -5. So we can initially say, the max(nums) is the max_product without knowing anything about the nums array.
1
max_product = max(nums)
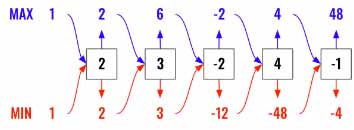
Now, please refer the diagram below. Here we are going to keep track of min and max product for every iteration of the loop. We need to compare 3 values.
MAX = max ( largest*nums[i],smallest*nums[i], nums[i])MIN = max ( largest*nums[i],smallest*nums[i], nums[i])
We need to consider the current value (nums[i]) as well for finding MIN and MAX. Notice above we have -2 as max and -12 as min. Now 4 could be the next MAX and not -8.
1
2
3
4
5
6
for i in range(len(nums)):
MAX = max ( largest*nums[i],smallest*nums[i], nums[i])
MIN = min ( largest*nums[i],smallest*nums[i], nums[i])
largest = MAX
smallest = MIN
max_product= max(max_product,largest)
We have one more edge case to take care. Whenever nums[i]==0 we need to reset largest and smallest otherwise all the products going forward will be 0.
1
2
3
4
5
6
for i in range(len(nums)):
if nums[i] ==0:
largest=1
smallest=1
continue
MAX = max( .... )
Finally just return the max_product.
1
return max_product
Final Code
Here is the full code.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def max_product(nums):
smallest, largest = 1, 1
max_product = max(nums)
for i in range(len(nums)):
if nums[i] ==0:
largest=1
smallest=1
continue
MAX = max ( largest*nums[i],smallest*nums[i], nums[i])
MIN = min ( largest*nums[i],smallest*nums[i], nums[i])
largest = MAX
smallest = MIN
max_product= max(max_product,largest)
return max_product