Dynamic Programming - Word Break

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

DP

Problem

Given a string s and a dictionary of strings wordDict, return true if s can be segmented into a space-separated sequence of one or more dictionary words.

Note that the same word in the dictionary may be reused multiple times in the segmentation.

Example 1:

Input: s = "leetcode", wordDict = ["leet","code"]
Output: true
Explanation: Return true because "leetcode" can be segmented as "leet code".

Example 2:

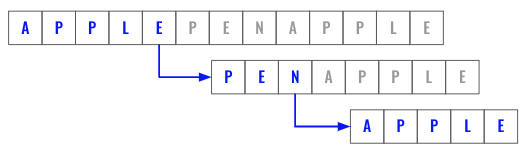
Input: s = "applepenapple", wordDict = ["apple","pen"]
Output: true
Explanation: Return true because "applepenapple" can be segmented as "apple pen apple".
Note that you are allowed to reuse a dictionary word.

Example 3:

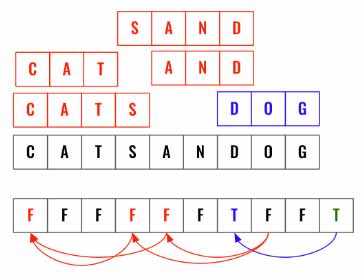
Input: s = "catsandog", wordDict = ["cats","dog","sand","and","cat"]
Output: false

Solution

DFS Solution

The DFS Solution works really well as we will be moving forward from left to right only when we find a matching word in wordDict. We can use memorization using a map which would make this as fast as dynamic programming. Let’s follow the template 2 that we have already discussed here.

Define the cache for memorization using map. Then define the dfs() function which takes truncated s.

cache={}

def dfs(s):
  ...

Let’s skip the base condition and focus on the actual algorithm first. Since we are using Template 2, we need to have a loop such that we are able to construct words using all the remaining letters as needed. We will start the loop from 1 so that we can keep increasing the window.

	for index in range(1, len(s)):

Now keep increasing the window by 1 and each time validate to see its there in wordDict, if there is match we will call dfs() again using remaining_s to repeat this again.

	for index in range(1, len(s)):
    window = s[:i]
    remaining_s = s[i:]
    if window in wordDict and dfs(remaining_s):
      ...

If the dfs() inside if returns True then there is a solution for remaining_s, so add remaining_s in cache. Now, we do not have to iterate through the for loop as we know we have a match, hence we will return True

    if window in wordDict and dfs(remaining_s):
    	cache[remaining_s]=True
      return True
      

At the end of for loop if the function has not returned then we know there is no solution for current s, so lets set that to the cache as False and return False.

	cache[s]=False
  return False

Finally, call the dfs() by passing s and return its return.

return dfs(s)

Now, it’s time to implement the base condition. If at anytime we have the final word then the current s will always be equal to one of the word present in wordDict. This will be the terminating condition.

def dfs(s):
  if s in wordDict:
    return True

Next, if we already have found a solution for s then just return that as well. If could be either True or False.

  if s in cache:
    return cache[s]

Dynamic Programming Solution

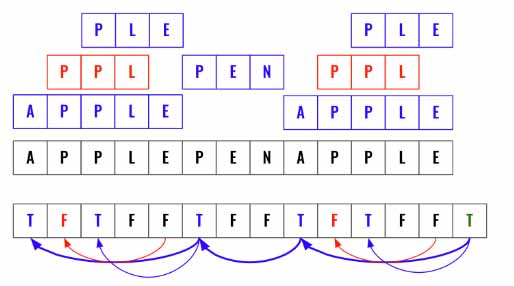
• Loop backward, all the True (matched words) needs to the connected.
• Fill each position in DP (Cache) using the previous discovered position. If the previous position is False then the current word is not useful. DP of that position will also be False.
• The bold line indicates success. Not all True values contribute to this.

Here is an example. At the bottom is the cache (DP). Initially all elements are set to False. Then have 2 loops to match each word at every index location and update DP (Cache) based one the previous ending value.

Here is another example where the output is False.

Let’s start by defining the dp cache array. The length of this needs to be 1+len(s) as we need to start using True at the end to move forward. This is going to be our base condition.

dp = [False] * (len(s)+1)
dp[-1] = True

Now we need to loop through s from backward and then try to match each word. If we have iterated enough to be equal or less then the length the current word in wordDict then only we can run the comparison.

for i in range(len(s)-1,-1,-1):
  for w in wordDict:
    if i+len(w) <=len(s):
    	if s[i:i+len(w)]==w:
        dp[i]=dp[i+len(w)]

If there is at least one match then we don’t have to continue looking for more words.

    if dp[i]:
    	break

Finally, return the output stored in dp[0].

Final Code

Here is the full code.

DFS Solution

def word_break(s, wordDict):
  cache={}
  def dfs(s):
    if s in wordDict:
    	return True 
	  if s in cache:
  	  return cache[s]    
    for index in range(1, len(s)):
      window = s[:i]
      remaining_s = s[i:]
      if window in wordDict and dfs(remaining_s):
        cache[remaining_s]=True
        return True
    cache[s]=False
    return False   
return dfs(s)

Dynamic Programming Solution

def word_break(s, wordDict):
  dp = [False] * (len(s)+1)
	dp[-1] = True
  
  for i in range(len(s)-1,-1,-1):
    for w in wordDict:
      if i+len(w) <=len(s):
        if s[i:i+len(w)]==w:
          dp[i]=dp[i+len(w)]
    if dp[i]:
    	break 
      
  return dp[0]