Dynamic Programming - Partition Equal Subset Sum
All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.
Difficulty : Easy
DP
Problem
Given an integer array nums, return true if you can partition the array into two subsets such that the sum of the elements in both subsets is equal or false otherwise.
Example 1:
1
2
3
Input: nums = [1,5,11,5]
Output: true
Explanation: The array can be partitioned as [1, 5, 5] and [11].
Example 2:
1
2
3
Input: nums = [1,2,3,5]
Output: false
Explanation: The array cannot be partitioned into equal sum subsets.
Solution
Before we get started with any solution, the following is very clear. We need to use the elements in any order and find if they could make two groups each having sum equal to target.
1
2
3
4
if sum(nums)%2==1:
return False
target = sum(nums)//2
DFS Solution
Seems fairly straightforward from a DFS solution standpoint. We can use template 2 that we have already discussed here.
The idea is not to find two sets of group, rather just find one path which leads to the target. Since we know the actual sum is double than the target then the remaining numbers must be added to make the other target value.
Now if we restructure the problem to this - “ Find if the elements of an array can make the target value when used only once”, it becomes much simpler to implement and we can use the same intuition when implementing using the dynamic programming approach.
Start with the terminating conditions, if the current target==0 then we know we have successfully reached to the end, so can return True, conversely if the target anytime is negative then we know we have overshoot the target and current path can not reach to a valid target, so we return False.
1
2
3
4
5
def dfs(index, target):
if target == 0:
return True
if target < 0:
return False
Now if we still have a positive target, we can loop and consider every other elements to find the target. If we ever find a True immediately return it. In case there is no success, return False at the end of the loop.
1
2
3
4
5
for j in range(index,len(nums)):
if dfs(j+1, target - nums[j]):
return True
return False
Finally call dfs() and return its return.
1
return dfs(0,target)
Even though this is a valid code, it will take O(2^n) time, hence won’t pass LeetCode, however we will use the similar concept below to implement using the dynamic programming.
Dynamic Programming
As discussed earlier we will use the same intuition. We need to find a target sum by using the numbers only once from an array. One way we can do this in O(n) time is for every element we find the sum for every combination. The space complexity will be large though.
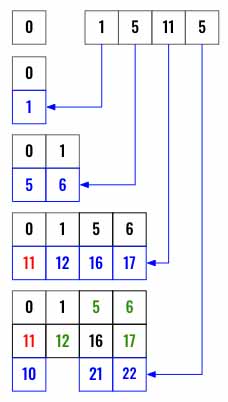
Below is an example, we are going to iterate through the array from left to right and keep all the summations in a set. Initially we start with a set having just a 0 as base case. Then we add 1 and keep both. Then we take 5, find the new summations and append them to the set as well (0 + 5 = 5, 1 + 5 = 6). We can keep doing this till the end of the loop.
If we have target in the set then we know we can reach it using the numbers to we return True. The best part is, we don’t even have to wait for the loop to complete, we can return True as soon as there is a target in the set.
1
2
3
4
5
6
7
8
9
10
cache = set([0])
for i in range(len(nums)):
copy_of_cache=cache.copy()
for digit in copy_of_cache:
cache.add(nums[i]+digit)
# We do not have to wait for the loop to complete.
if target in cache:
return True
return False
Final Code
Here is the full code.
DFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def can_partition(nums):
if sum(nums) % 2 == 1:
return False
target = sum(nums)//2
def dfs(index, target):
if target == 0:
return True
if target < 0:
return False
for j in range(index,len(nums)):
if dfs(j+1, target - nums[j]):
return True
return False
return dfs(0, target)
Dynamic Programming
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def can_partition(nums):
if sum(nums) % 2 == 1:
return False
target = sum(nums)//2
cache = set([0])
for i in range(len(nums)):
copy_of_cache = cache.copy()
for digit in copy_of_cache:
cache.add(nums[i]+digit)
# We do not have to wait for the loop to complete.
if target in cache:
return True
return False