Dynamic Programming - Min Cost Climbing Stairs

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

DP

Problem

You are given an integer array cost where cost[i] is the cost of ith step on a staircase. Once you pay the cost, you can either climb one or two steps. You can either start from the step with index 0, or the step with index 1. Return the minimum cost to reach the top of the floor.

Example 1:

Input: cost = [10,15,20]
Output: 15
Explanation: You will start at index 1.
- Pay 15 and climb two steps to reach the top.
The total cost is 15.

Example 2:

Input: cost = [1,100,1,1,1,100,1,1,100,1]
Output: 6
Explanation: You will start at index 0.
- Pay 1 and climb two steps to reach index 2.
- Pay 1 and climb two steps to reach index 4.
- Pay 1 and climb two steps to reach index 6.
- Pay 1 and climb one step to reach index 7.
- Pay 1 and climb two steps to reach index 9.
- Pay 1 and climb one step to reach the top.
The total cost is 6.

Solution

First, let’s think in terms of a dfs problem. We can use the template 2 that we have already discussed here.

At every step we can call our dfs() function twice and find which path leads to min cost to reach the top of the floor. This is very similar to the Climbing Stairs, similarly we will add an additional 0 to cost as we did in the Climbing Stairs problem for the base case to work.

 cost.append(0)     

Define a min_cost variable.

min_cost=float('inf')

In the dfs() function, we pass the current index and curr_cost. Our base condition is whenever index==len(cost) , we can compare curr_cost with min_cost.

def dfs(index,curr_cost):
  nonlocal min_cost
  if index == len(cost):
    min_cost = min(min_cost,curr_cost)
    return     

Now we need to have a loop runs only twice.

for j in range(index, min(index+2,len(cost))):

Inside the loop, we increment curr_cost, call dfs() again and backtrack curr_cost.

for j in range(index, min(index+2,len(cost))):
  curr_cost+=cost[j]                
  dfs(j+1,curr_cost)                
  curr_cost-=cost[j]

At the end, call dfs(0,0) and return min_cost. (Full code at the end)

dfs(0,0)
return min_cost

Unfortunately even though the code is all good, the solution won’t pass the Leetcode as it will takes $O(2^n)$ time and Leetcode will expect the solution to be competed in $O(n)$ time.

Dynamic Programming

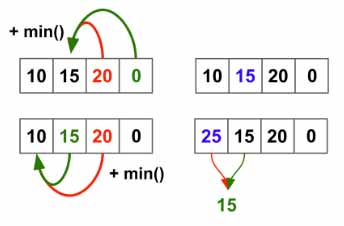
Idea to solve using Dynamic Programming is to start from backward (This is a patten in general). Consider the first example, we need to evaluate to find out if 20 or 15 is a place to be in. What we will do it, just a 0 at the end for the loop. Then for 15 find the min between 20 and 0. Set that as the new cost for 15. Now do the same for 10. The updated cost for 10 will be 10+15=25.

cost.append(0)
for i in range(len(cost)-3,-1,-1):
  cost[i]+= min(cost[i+1],cost[i+2])
  

Finally return the min cost from first or second location.

return min(cost[0],cost[1])

Final Code

Here is the full code.

DFS/Backtrack Solution

def min_cost_climbing_stairs(cost):
    min_cost = float('inf')
    cost.append(0)

    def dfs(index, curr_cost):
        nonlocal min_cost
        if index == len(cost):
            min_cost = min(min_cost, curr_cost)
            return
        for j in range(index, min(index+2, len(cost))):
            curr_cost += cost[j]
            dfs(j+1, curr_cost)
            curr_cost -= cost[j]
    dfs(0, 0)

    return min_cost

Dynamic Programming Solution

def min_cost_climbing_stairs(cost):
  cost.append(0)
  for i in range(len(cost)-3,-1,-1):
    cost[i]+= min(cost[i+1],cost[i+2])

  return min(cost[0],cost[1])