Dynamic Programming - Coin Change

All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.

Difficulty : Easy

DP

Problem

You are given an integer array coins representing coins of different denominations and an integer amount representing a total amount of money.

Return the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.

You may assume that you have an infinite number of each kind of coin.

Example 1:

Input: coins = [1,2,5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1

Example 2:

Input: coins = [2], amount = 3
Output: -1

Example 3:

Input: coins = [1], amount = 0
Output: 0

Solution

DFS/Backtracking Solution

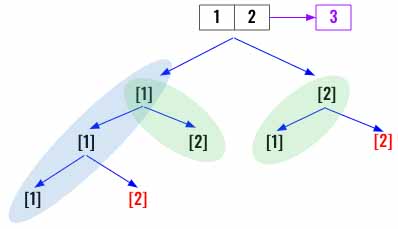
We will first find out how to solve this problem using DFS/Backtracking solution. Consider an example where coins=[1,2] and amount= 3. At every step until we have reached or exceeded the amount we can keep adding each of the coins to the total. Then once we have reached the total we can find the min path.

We will start by defining the min_path variable.

min_path=float("inf")

Now define the dfs() function. It takes the remaining amount and the current path as inputs. If the remaining amount is less then amount we return however if its same as remaining then we find the len(path) and update min_path if needed.

 def dfs(remaining,path):            
    nonlocal min_path            
    if remaining < 0:
      return
    if remaining==0:
      min_path=min(min_path,len(path))

Now loop through all the coins and add the each coin to path then after recursively calling dfs() backtrack the added coin from the path.

    for coin in coins:
      path.append(coin)
      dfs(remaining - coin, path)
      path.pop()

Finally, call dfs() and return min_path.

dfs(amount,[])                
return min_path if min_path!=float("inf") else -1

Even though this is a proper solution, however the time complexity is very high $N^{\text{amount}}$ , where N is the number of different coin denominations. There is a more complex way of implementing this using memoization, however we are going to directly look into the DP solution next.

Dynamic Programming

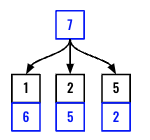
The idea again comes down to breaking the problem in smaller problem. Like we have done in the previous problems, let’s consider coins = [1,2,5] and amount = 7 as an example.

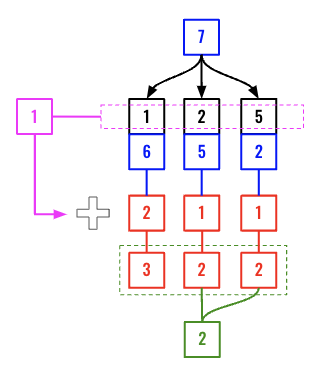
We need to find out, whats the fewest number of coins to make 7? Since we have coins with value 1,2,5 we can subtract each coin from 7. Referring the diagram below, if we know the fewest number of coins to make 6,5 & 2 when we can just add 1 to that number and find the min among them.

If we know that the fewest number of coins to make 6,5 & 2 are respectively 2,1 and 1 then we can add 1 to that number as we have used 1,2,5 once (pink arrow below). So the final values are 3,2,2. Now we can take min among them and the final result is 2. (Either 7-2=5 or 7-5=2)

The only unknown part here is how do we know the fewest number of coins to make 6,5 & 2? These numbers can also be anything (based on the coins array). However we know that these numbers will always be less than amount. So if we can have the fewest number of coins to make all the values from 0 - (amount-1) then in the final step will need just O(n) to find the final result. (Here n is length of coins).

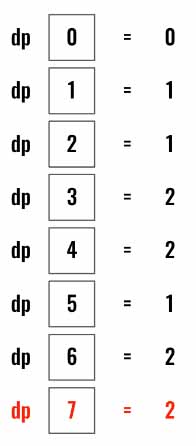
In this example, we will calculate all the values in a loop. (Refer below).

This is the main logic, where we have two for loops. One for finding fewest number of coins to make for each amounts from 0 - amount.

for prev_amount in range(1, amount+1):
  for coin in coins:
    if prev_amount - coin >=0:
      cache[prev_amount]=min(cache[prev_amount], 1+ cache[prev_amount - coin])

Initially we will create the cache with float("inf") values with length amount+1 and will set cache[0]=0.

cache = [float("inf")]*(amount+1)
cache[0]=0

Following are the patterns used here to find the DP solution.

• 1D DP Problem
• 2D DP Problem
• Backward
• Break into smaller problem
• PreCompute values
• Caching

Final Code

Here is the full code.

def coin_change(coins, amount):
  cache = [float("inf")]*(amount+1)
  cache[0]=0
  
  for prev_amount in range(1, amount+1):
    for coin in coins:
      if prev_amount - coin >=0:
        cache[prev_amount]=min(cache[prev_amount], 1+ cache[prev_amount - coin])
        
  return cache[amount] if cache[amount]!=float("inf") else -1