Dynamic Programming - Climbing Stairs
All diagrams presented herein are original creations, meticulously designed to enhance comprehension and recall. Crafting these aids required considerable effort, and I kindly request attribution if this content is reused elsewhere.
Difficulty : Easy
DP
Problem
You are climbing a staircase. It takes n steps to reach the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
Example 1:
1
2
3
4
5
Input: n = 2
Output: 2
Explanation: There are two ways to climb to the top.
1. 1 step + 1 step
2. 2 steps
Example 2:
1
2
3
4
5
6
Input: n = 3
Output: 3
Explanation: There are three ways to climb to the top.
1. 1 step + 1 step + 1 step
2. 1 step + 2 steps
3. 2 steps + 1 step
Solution
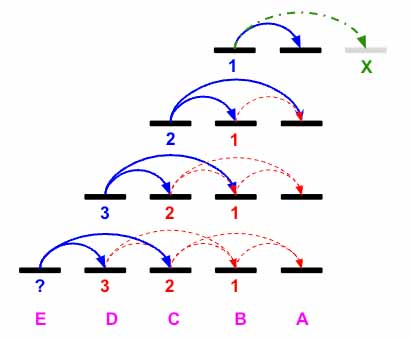
The problem is easy to understand so let’s first visualize it. Say we have 4 stairs named A,B,C,D,E. The goal is to reach A. Now from B we can reach 1 way, thats making one jump. If we make two jumps thats out of bound.
- Now from
Cwe can reachBby one jump and toAusing a double jump. So total fromCwe can reachAin2ways. - From
D, we can reachCby one jump and we already know that fromCwe have2ways to reachA. We also can reachBfromCusing a double jump and fromBwe can reachAin just1way. So in total we can reachAfromDusingD->CandD->B, which is2 + 1 = 3ways. - I hope you see a pattern. From
E, we can reachAusing two waysE->DandE->C. Now fromDwe already know we have3ways to reach and fromCwe have2ways to reachA. So is we sum, there are3+2=5ways to reach fromE->A
Let’s use this concept to solve the problem first. We know E=D+C, D=C+B, however what is C=B+?. Imagine if one above the top is X (shown in above pic) then the value of X will be 0 as you are already at the top. Hence setting X=0, we get C=B+A. So if we set A=1 and X=0 then C=1+1=2 and B=A+X =1+0 =1
So we can write the equations as $F_n = F_{n-1}+F_{n-2}$. Imagine $F_{n-1}$ to be initially A and $F_{n-2}$ to X.
1
2
3
4
5
6
7
F1,F2 = 1,0
for _ in range(n):
T=F1
F1=F1+F2
F2=T
return F1
This problem can be solved using a recursive solution which we will explore now. It’s a similar concept, however instead of starting from back, we are going to use recursion to explore from beginning and using call stack to reverse calculate from the base condition of when curr_step==n then return 1 and when curr_step >n return 0 (This is simulating X=0 in the DP solution).
The function will take curr_steps as an input and in every iteration we are going to find out the steps as function(curr_steps+1)+function(curr_steps+2) as defined by the problem itself.
1
2
3
4
5
6
7
8
9
10
def recursive_func(curr_steps):
if curr_steps == n:
return 1
if curr_steps>n:
return 0
steps = recursive_func(curr_steps+1)+recursive_func(curr_steps+2)
return steps
We shall cache the values so that program can run faster. Here is code where are caching the input curr_steps and output steps
1
2
3
4
5
6
7
8
9
10
11
12
13
14
cache = {}
def recursive_func(curr_steps):
if curr_steps == n:
return 1
if curr_steps>n:
return 0
if curr_steps in cache:
return cache[curr_steps]
steps = recursive_func(curr_steps+1)+recursive_func(curr_steps+2)
cache[curr_steps] = steps
return steps
Final Code
Here is the full code.
Dynamic Programming
1
2
3
4
5
6
7
def climbing_stairs(n):
F1,F2 = 1,0
for _ in range(n):
T=F1
F1=F1+F2
F2=T
return F1
Recursive Method
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def climbing_stairs(n):
cache = {}
def recursive_func(curr_steps):
if curr_steps == n:
return 1
if curr_steps>n:
return 0
if curr_steps in cache:
return cache[curr_steps]
steps = recursive_func(curr_steps+1)+recursive_func(curr_steps+2)
cache[curr_steps] = steps
return steps
return climbing_stairs(0)